决策树的剪枝算法

发表于 | 分类于

在知道怎么得到一颗决策树后、我们当然就会想知道：这样建立起来的决策树的表现究竟如何？从直观上来说，只要决策树足够深、划分标准足够细，它在训练集上的表现就能接近完美；但同时也容易想象，由于它可能把训练集的一些“特性”当做所有数据的“共性”来看待，它在未知的测试数据上的表现可能就会比较一般、亦即会出现过拟合的问题。我们知道，模型出现过拟合问题一般是因为模型太过复杂，所以决策树解决过拟合的方法是采取适当的“剪枝”、我们在上一篇文章中也已经大量接触了这一概念。剪枝通常分为两类：“预剪枝（Pre-Pruning）”和“后剪枝（Post-Pruning）”，其中“预剪枝”的概念在生成算法中已有定义，彼时我们采取的说法是“停止条件”；而一般提起剪枝时指的都是“后剪枝”，它是指在决策树生成完毕后再对其进行修剪、把多余的节点剪掉。换句话说，后剪枝是从全局出发、通过某种标准对一些 Node 进行局部剪枝，这样就能减少决策树中 Node 的数目、从而有效地降低模型复杂度

是故问题的关键在于如何定出局部剪枝的标准。通常来说我们有两种做法：

  • 应用交叉验证的思想，若局部剪枝能够使得模型在测试集上的错误率降低、则进行局部剪枝（预剪枝中也应用了类似的思想）
  • 应用正则化的思想、综合考虑不确定性和模型复杂度来定出一个新的损失（此前我们的损失只考虑了不确定性），用该损失作为一个 Node 是否进行局部剪枝的标准

第二种做法又涉及到另一个关键问题：如何定量分析决策树中一个 Node 的复杂度？一个直观且合理的方法是：直接使用该 Node 下属叶节点的个数作为复杂度。基于此、第二种做法的数学描述就是：

  • 定义新损失（代表一个 Node） 其中，即是该 Node 和不确定性相关的损失、则是该 Node 下属叶节点的个数。不妨设第 t 个叶节点含有个样本且这个样本的不确定性为，那么新损失一般可以直接定义为加权不确定性：

我们会采取这种做法来进行实现。需要指出的是，在这种做法下、仍然可以分支出两种不同的算法：

  • 直接比较一个 Node 局部剪枝前的损失和局部剪枝后的损失的大小，若：
  • 获取一系列的剪枝阈值：，在每个剪枝阈值上对相应的 Node 进行局部剪枝并将局部剪枝后得到的决策树储存在一个列表中。在上我们会对根节点进行局部剪枝，此时剩下来的决策树就只包含根节点这一个 Node。最后，通过交叉验证选出中最好的决策树作为最终生成的决策树（注意其中的即是没有剪过枝的原始树）

第一种算法清晰易懂，第二种算法则稍显复杂；一般我们会在 ID3 和 C4.5 中应用第一种剪枝算法、在 CART 中应用第二种剪枝算法。上述这个第二种算法的说明可能有些过于简略、让人摸不着头脑；由于详细的算法叙述会在后文再次进行，所以这里只要有一个大概的直观感受即可，细节可以暂时按下、不必太过纠结

ID3、C4.5 的剪枝算法

首先我们来看看第一种算法的详细叙述。虽说算法本身的思想很简单，但由于其中涉及到许多中间变量、所以我们采取类似于伪代码的形式来进行叙述：

  1. 输入：生成算法产生的原始决策树，惩罚因子
  2. 过程：
    1. 从下往上地获取中所有 Node，存入列表_tmp_nodes
    2. 对_tmp_nodes中的所有 Node 计算损失，存入列表_old
    3. 计算_tmp_nodes中所有 Node 进行局部剪枝后的损失，存入列表_new
    4. 进入循环体：
      1. 若_new中所有损失都大于_old中对应的损失、则退出循环体
      2. 否则，设 p 满足： 则对_tmp_nodes[p]进行局部剪枝
      3. 在完成局部剪枝后，更新_old、_new、_tmp_nodes等变量。具体而言，我们无需重新计算它们、只需更新“被影响到的” Node 所对应的位置的值即可
    5. 最后调用self.reduce_nodes方法、将被剪掉的 Node 从nodes中除去
  3. 输出：修剪过后的决策树

我们可以在我们之前用气球数据集 1.0 根据 ID3 算法生成的决策树上过一遍剪枝算法以加深理解。由于算法顺序是从下往上、所以我们先考察最右下方的 Node（该 Node 的划分标准是“测试人员”），该 Node 所包含的数据集如下表所示：

颜色 测试人员 结果
黄色 成人 爆炸
黄色 小孩 不爆炸

从而：

  • 局部剪枝前、该 Node 的损失为：
  • 局部剪枝后、该 Node 的损失为： 其中 故

回忆生成算法的实现，我们彼时将定义为了（注意：这只是的一种朴素的定义方法，很难说它有什么合理性、只能说它从直观上有一定道理；如果想让模型表现更好、需要结合具体的问题来分析应该取何值）。由于气球数据集 1.0 一共有四个特征、所以此时；结合各个公式、我们发现：

所以我们应该对该 Node 进行局部剪枝。局部剪枝后的决策树如下图所示：

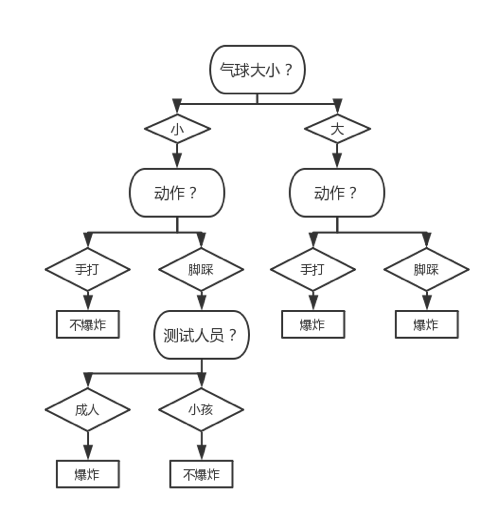
p1.png

注意：进行局部剪枝后，由于该 Node 中样本只有两个、且一个样本类别为“不爆炸”一个为“爆炸”，所以给该 Node 标注为“不爆炸”、“爆炸”甚至以 50%的概率标注为“不爆炸”等做法都是合理的。为简洁，我们如上图中所做的一般、将其标注为“爆炸”

然后我们需要考察最左下方的 Node（该 Node 的划分标准也是“测试人员”），易知计算过程和上述的没有区别。对其进行局部剪枝后的决策树如下图所示：

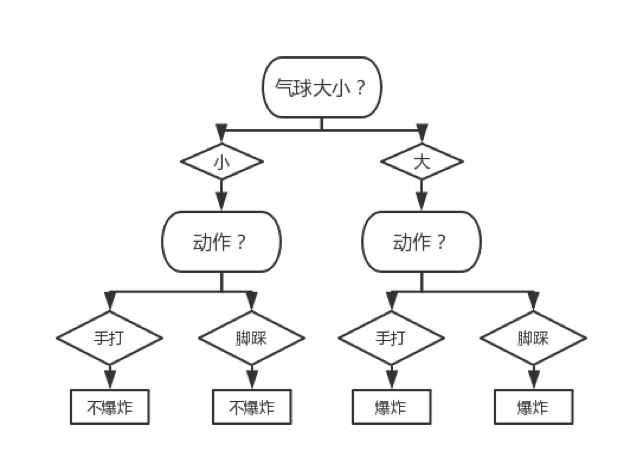
p2.png

然后我们需要考察右下方的 Node（该 Node 的划分标准是“动作”），该 Node 所包含的数据集如下表所示：

颜色 测试人员 测试动作 结果
黄色 成人 用手打 爆炸
黄色 成人 用脚踩 爆炸
黄色 小孩 用手打 不爆炸
黄色 小孩 用脚踩 爆炸
紫色 成人 用脚踩 爆炸
紫色 小孩 用脚踩 爆炸

从而：

  • 局部剪枝前、该 Node 的损失为：

    其中

    故

  • 局部剪枝后、该 Node 的损失为： 其中 故

将代入、知：

故应该对该 Node 进行局部剪枝。局部剪枝后的决策树如下图所示：

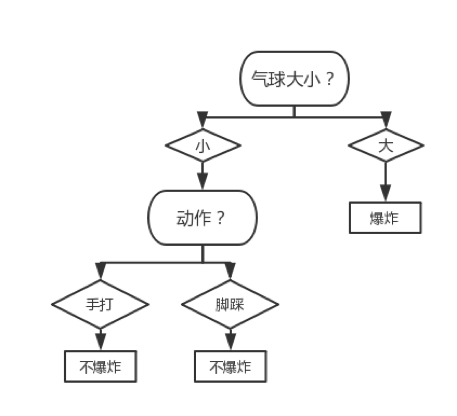
p3.png

然后我们需要考察左下方的 Node（该 Node 的划分标准也是“动作”），易知计算过程和上述的没有区别。对其进行局部剪枝后的决策树如下图所示：

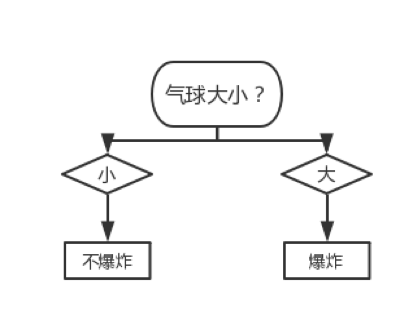
p4.png

通过计算易知不应对根节点进行局部剪枝、所以上图所示的决策树即是当时最终修剪出来的决策树

CART 剪枝

第二种剪枝算法（CART 剪枝）中的许多定义可能还不是很清晰，所以我们先对相关概念进行详细一点的直观说明：

首先需要指出的是：关于第二种算法中出现的一系列的阈值，它们的含义其实和第一种算法中的一样、都是模型复杂度的“惩罚因子”；不同的是，第一种算法的是人为给定的、第二种算法中一系列的阈值则是算法生成出来的。其中，意味着算法初始不对模型复杂度进行惩罚、此时最优树即是原始树。然后我们设想缓慢增大、亦即缓慢增大对模型复杂度的惩罚，那么到某个阈值时，对决策树中某个 Node 进行局部剪枝就是一个更好的选择。我们将该 Node 进行局部剪枝后的决策树存进一个列表中、然后继续缓慢增加惩罚因子，继而到某个阈值后、对某个 Node 进行局部剪枝就又会是一个更好的选择……以此类推，直到变成一个充分大的数后、只保留根节点这一个 Node 会是最好的选择，此时就终止算法并通过交叉验证从中选出最好的作为修剪后的决策树。

那么这个相对比较复杂的算法有什么优异之处呢？可以证明：在 CART 剪枝里得到的决策树中，对、都是当惩罚因子时的最优决策树。这条性质保证了 CART 算法最终通过交叉验证选出来的决策树具有一定的优良性。

该算法的详细叙述则如下：

  1. 输入：在训练集上调用生成算法所产生的原始决策树，交叉验证集
  2. 过程：
    1. 从下往上地获取中所有 Node，存入列表_tmp_nodes
    2. 对_tmp_nodes中的所有 Node 计算阈值，存入列表_thresholds；其中，第 t 个 Node 的阈值应满足： 其中即是第 t 个 Node 自身数据的不确定性；换言之，代表着第 t 个 Node 进行局部剪枝前的新损失、代表着局部剪枝后的新损失。由上式可求出： 此即阈值的计算公式
    3. 进入循环体：
      1. 将当前决策树存入列表self.roots
      2. 若当前决策树中只剩根节点、则退出循环体
      3. 否则，取 p 满足： 然后对_tmp_nodes[p]进行局部剪枝
      4. 在完成局部剪枝后，更新_thresholds、_tmp_nodes等变量。具体而言，我们无需重新计算它们、只需更新“被影响到的” Node 所对应的位置的值即可
    4. 然后调用self.reduce_nodes方法、将被剪掉的 Node 从nodes中除去
    5. 最后利用交叉验证、从self.roots中选出表现最好的决策树
  3. 输出：修剪过后的决策树
观众老爷们能赏个脸么 ( σ'ω')σ