本篇文章将简要说明几种将二分类模型拓展为多分类模型的普适性方法,它们不仅能对前三篇文章叙述的感知机和 SVM 进行应用、同时还能应用于在上一个系列中进行了说明的 AdaBoost 二分类模型;在本篇的第四节(也是最后一节)、我们则会简要地说明一下如何将支持向量机的思想应用在回归问题上
一对多方法(One-vs-Rest)
一对多方法常简称为 OvR、是一种比较比较“豪放”的方法:对于一个 K 类问题、OvR 将训练 K 个二分类模型,每个模型将训练集中的某一类的样本作为正样本、其余类的样本作为负样本。模型的输出空间为实数空间、它反映了模型对决策的“信心”
具体而言、模型会把第类看成一类、把其余类看成另一类并尝试通过训练来区分开第类和剩余类别;若有比较大的自信来判定输入样本x是(或不是)第类、那么将会是一个比较大的正(负)数,否则、将会是一个比较小的正(负)数
训练好 K 个模型后、直接将输出最大的模型所对应的类别作为决策即可、亦即:
之所以称这种方法比较“豪放”、主要是因为对每个模型的训练都存在比较严重的偏差:正样本集和负样本集的样本数之比在原始训练集均匀的情况下将会是。针对该缺陷、一种比较常见的做法是只抽取负样本集中的一部分来进行训练(比如抽取其中的三分之一)
一对一方法(One-vs-One)
一对一方法常简称为 OvO、可谓是一种很直观的方法:对于一个 K 类问题、OvO 将直接训练出个二分类模型,每个模型都只从训练集中接受两个类的样本来进行训练。模型的输出空间为二值空间、亦即模型只需要具有投票的能力即可
具体而言、模型将接受且仅接受所有第类和第类的样本并尝试通过训练来区分开第类和第类;同时,假设代表第类的样本空间、那么就有:
训练好个模型后,OvO 将通过投票表决来进行决策、在次投票中得票最多的类即为模型所预测的结果。具体而言,如果考察、那么若输出则第类得一票、若输出则第类得一票。如果只有两个类别(比如第类和第类)得票一致、那么直接看针对这两个类别的模型(亦即)的结果即可;如果多于两个类别的得票一致、则需要具体情况具体分析
OvO 是一个相当不错的方法、没有类似于 OvR 中“有偏”的问题。然而它也是有一个显而易见的缺点的——由于模型的量级是、所以它的时间开销会相当大
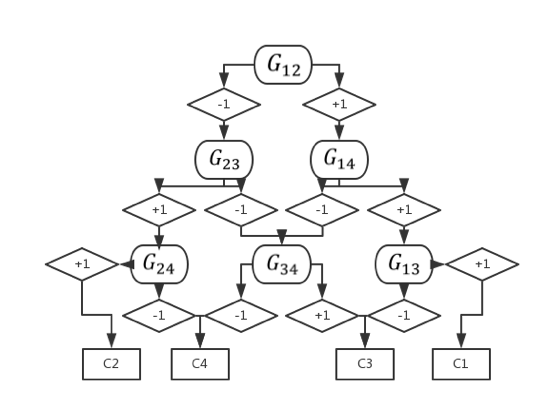
有向无环图方法(Directed Acyclic Graph Method)
有向无环图方法常简称为 DAG,它的训练过程和 OvO 的训练过程完全一致、区别只在于最后的决策过程。具体而言、DAG 会将个模型作为一个有向无环图中的节点并逐步进行决策。其工作原理可以用下图进行说明(假设):
支持向量回归(Support Vector Regression)
支持向量回归常简称为 SVR,它的基本思想与“软”间隔的思想类似——传统的回归模型通常只有在模型预测值和真值完全一致时损失函数的值才为 0(最经典的就是当损失函数为的情形),而 SVR 则允许和之间有一个的误差、亦即仅当:
时、我们才认为模型在点处有损失。这与支持向量机做分类时有种“恰好相反”的感觉:对于分类问题、只有当样本点离分界面足够远时才不计损失;对于回归问题、则只有当真值离预测值足够远时才计损失。但是仔细思考的话、就不难想通它们的思想和目的是完全一致的:都是为了提高模型的泛化能力
类比于之前讲过的 SVM 算法、可以很自然地写出 SVR 所对应的无约束优化问题:
其中
于是可以利用梯度下降法等进行求解。同样类比于 SVM 的对偶问题、我们可以提出 SVR 的对偶问题,细节就不展开叙述了

