利用 Tensorflow 重写 NN

发表于 | 分类于

本文将会使用 Tensorflow 框架来重写我们上个系列中实现过的 NN、观众老爷们可能会需要知道 Tensorflow 的基本知识之后才能比较顺畅地阅读接下来的内容；如果对 Tensorflow 基本不了解的话、可以先参见我写的一篇 Tensorflow 的应用式入门教程

重写 Layer 结构

使用 Tensorflow 来重写 NN 的流程和上个系列中我们介绍过的实现流程是差不多的，不过由于 Tensorflow 帮助我们处理了更新参数这一部分的细节，所以我们能增添许多功能、同时也能把接口写得更漂亮一些。

首先还是要来实现 NN 的基本单元——Layer 结构。鉴于 Tensorflow 能够自动获取梯度、同时考虑到要扩展出 CNN 的功能，我们需要做出如下微调：

  • 对于激活函数，只用定义其原始形式、不必定义其导函数形式
  • 解决上一章遗留下来的、特殊层结构的实现问题
  • 要考虑当前层为 FC（全连接层）时的表现
  • 让用户可以选择是否给 Layer 加偏置量

其中的第四点可能有些让人不明所以：上个系列不是刚说过、偏置量对破坏对称性是很重要的吗？为什么要让用户选择是否使用偏置量呢？这主要是因为特殊层结构中 Normalize 的特殊性会使偏置量显得冗余。具体细节会在后文讨论特殊层结构处进行说明，这里就暂时按下不表

以下是 Layer 结构基类的具体代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
import numpy as np
import tensorflow as tf
from math import ceil
class Layer:
    """
        初始化结构
        self.shape：记录该Layer和上个Layer所含神经元的个数，具体而言：
            self.shape[0] = 上个Layer所含神经元的个数
            self.shape[1] = 该Layer所含神经元的个数
        self.is_fc、self.is_sub_layer：记录该Layer是否为FC、特殊层结构的属性
        self.apply_bias：记录是否对该Layer加偏置量的属性
    """
    def __init__(self, shape, **kwargs):
        self.shape = shape
        self.is_fc = self.is_sub_layer = False
        self.apply_bias = kwargs.get("apply_bias", True)
    def __str__(self):
        return self.__class__.__name__
    def __repr__(self):
        return str(self)
    @property
    def name(self):
        return str(self)
    @property
    def root(self):
        return self
    # 定义兼容特殊层结构和CNN的、前向传导算法的封装
    def activate(self, x, w, bias=None, predict=False):
        # 如果当前层是FC、就需要先将输入“铺平”
        if self.is_fc:
            x = tf.reshape(x, [-1, int(np.prod(x.get_shape()[1:]))])
        # 如果是特殊的层结构、就调用相应的方法获得结果
        if self.is_sub_layer:
            return self._activate(x, predict)
        # 如果不加偏置量的话、就只进行矩阵相乘和激活函数的作用
        if not self.apply_bias:
            return self._activate(tf.matmul(x, w), predict)
        # 否则就进行“最正常的”前向传导算法
        return self._activate(tf.matmul(x, w) + bias, predict)
    # 前向传导算法的核心、留待子类定义
    def _activate(self, x, predict):
        pass

注意到我们前向传导算法中有一项“predict”参数，这主要是因为特殊层结构的训练过程和预测过程表现通常都会不一样、所以要加一个标注。该标注的具体意义会在后文进行特殊层结构 SubLayer 的相关说明时体现出来、这里暂时按下不表

在实现好基类后、就可以实现具体要用在神经网络中的 Layer 了。以 Sigmoid 激活函数对应的 Layer 为例：

1
2
3
class Sigmoid(Layer):
    def _activate(self, x, predict):
        return tf.nn.sigmoid(x)

得益于 Tensorflow 框架的强大（你除了这句话就没别的话说了吗……）、我们甚至连激活函数的形式都无需手写，因为它已经帮我们封装好了（事实上、绝大多数常用的激活函数在 Tensorflow 里面都有封装）

实现特殊层

这一节我们将介绍如何利用 Tensorflow 框架实现上个系列没有实现的特殊层结构——SubLayer，同时也会对十分常用的两种 SubLayer（Dropout、Normalize）做比上个系列深入一些的介绍

先来看看应该如何定义 SubLayer 的基类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 让SubLayer继承Layer以合理复用代码
class SubLayer(Layer):
    """
        初始化结构
        self.shape：和Layer相应属性意义一致
        self.parent：记录该Layer的父层的属性
        self.description：用于可视化的属性，记录着对该SubLayer的“描述”
    """
    def __init__(self, parent, shape):
        Layer.__init__(self, shape)
        self.parent = parent
        self.description = ""
    # 辅助获取Root Layer的property
    @property
    def root(self):
        _root = self.parent
        while _root.parent:
            _root = _root.parent
        return _root

可以看到，得益于 Tensorflow 框架（Tensorflow 就是很厉害嘛……），本来难以处理的SubLayer 的实现变得非常简洁清晰。在实现好基类后、就可以实现具体要用在神经网络中的 SubLayer 了，先来看 Dropout：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Dropout(SubLayer):
    # self._prob：训练过程中每个神经元被“留下”的概率
    def __init__(self, parent, shape, drop_prob=0.5):
        # 神经元被Drop的概率必须大于等于0和小于1
        if drop_prob < 0 or drop_prob >= 1:
            raise ValueError(
                "(Dropout) Probability of Dropout should be a positive float smaller than 1")
        SubLayer.__init__(self, parent, shape)
        # 被“留下”的概率自然是1-被Drop的概率
        self._prob = tf.constant(1 - drop_prob, dtype=tf.float32)
        self.description = "(Drop prob: {})".format(drop_prob)
    def _activate(self, x, predict):
        # 如果是在训练过程，那么就按照设定的、被“留下”的概率进行Dropout
        if not predict:
            return tf.nn.dropout(x, self._prob)
        # 如果是在预测过程，那么直接返回输入值即可
        return x

Dropout 的详细说明自然是看原 paper 最好，这里我就大概翻译、总结一下主要内容。Dropout 的核心思想在于提高模型的泛化能力：它会在每次迭代中依概率去掉对应 Layer 的某些神经元，从而每次迭代中训练的都是一个小的神经网络。这个过程可以通过下图进行说明：

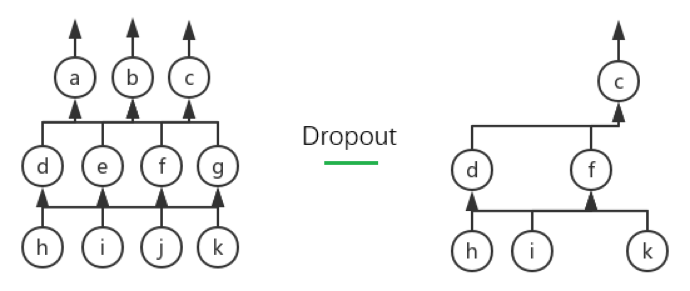
p1.png

上图所示的即为当drop_prob为 50%（我们所设的默认值）时、Dropout 的一种可能的表现。左图所示为原网络、右图所示的为 Dropout 后的网络，可以看到神经元 a、b、e、g、j 都被 Drop 了

Dropout 过程的合理性需要概率论上一些理论的支撑，不过鉴于 Tensorflow 框架有封装好的相应函数、我们就不深入介绍其具体的数学原理而仅仅说明其直观（以drop_prob为 50%为例，其余drop_prob的情况是同理的）：

  • 在训练过程中，由于 Dropout 后留下来的神经元可以理解为“在 50%死亡概率下幸存”的神经元，所以给将它们对应的输出进行“增幅”是合理的。具体而言，假设一个神经元的输出本来是，那么如果 Dropout 后它被留下来了的话、其输出就应该变成（换句话说、应该让带 Dropout 的期望输出和原输出一致：对于任一个神经元，设drop_prob为而其原输出为，那么当带 Dropout 的输出为时、的期望输出即为）
  • 由于在训练时我们保证了神经网络的期望输出不变、所以在预测过程中我们还是应该让整个网络一起进行预测而不进行 Dropout（关于这一点，原论文似乎也表示这是一种“经试验证明行之有效”的办法而没有给出具体的、原理层面的说明）

接下来介绍一下 Normalize。Normalize 这个特殊层结构的学名叫 Batch Normalization、常简称为 BN，顾名思义，它用于对每个 Batch 对应的数据进行规范化处理。这样做的意义是直观的：对于 NN、CNN 乃至任何机器学习分类器来说，其目的可以说都是从训练样本集中学出样本在样本空间中的分布、从而可以用这个分布来预测未知数据所属的类别。如果不对每个 Batch 的数据进行任何操作的话，不难想象它们彼此对应的“极大似然分布（极大似然估计意义下的分布）”是各不相同的（因为训练集只是样本空间中的一个小抽样、而 Batch 又只是训练集的一个小抽样）；这样的话，分类器在接受每个 Batch 时都要学习一个新的分布、然后最后还要尝试从这些分布中总结出样本空间的总分布，这无疑是相当困难的。如果存在一种规范化处理方法能够使每个 Batch 的分布都贴近真实分布的话、对分类器的训练来说无疑是至关重要的

传统的做法是对输入进行很久以前提到过的归一化处理、亦即：

其中表示的均值、表示的标准差（Standard Deviation）。这种做法虽然能保证输入数据的质量、但是却无法保证NN里面中间层输出数据的质量。试想NN中的第一个隐藏层，它接收的输入是输入层的输出和权值矩阵相乘后、加上偏置量后的结果；在训练过程中，虽然的质量有保证，但由于和在训练过程中会不断地被更新、所以的分布其实仍然不断在变。换句话说、的质量其实就已经没有保证了

BN 打算解决的正是随着前向传导算法的推进、得到的数据的质量会不断变差的问题，它能通过对中间层数据进行某种规范化处理以达到类似对输入归一化处理的效果。事实上回忆上一章的内容、我们已经提到过 Normalize 的核心思想在于把父层的输出进行“归一化”了，下面我们就简单看看它具体是怎么做到这一点的

首先需要指出的是，简单地将每层得到的数据进行上述归一化操作显然是不可行的、因为这样会破坏掉每层自身学到的数据特征。设想如果某一层学到了“数据基本都分布在样本空间的边缘”这一特征，这时如果强行做归一化处理并把数据都中心化的话、无疑就摈弃了所学到的、可能是非常有价值的知识

为了使得中心化之后不破坏 Layer 本身学到的特征、BN 采取了一个简单却十分有效的方法：引入两个可以学习的“重构参数”以期望能够从中心化的数据重构出 Layer 本身学到的特征。具体而言：

  1. 输入：某一层在当前 Batch 上的输出、增强数值稳定性所用的小值
  2. 过程：
    1. 计算当前 Batch 的均值、方差：
    2. 归一化：
    3. 线性变换：
  3. 输出：规范化处理后的输出

BN 的核心即在于、这两个参数的应用上。关于如何利用反向传播算法来更新这两个参数的数学推导会稍显繁复、我们就不展开叙述了，取而代之、我们会直接利用 Tensorflow 来进行相关的实现

需要指出的是、对于算法中均值和方差的计算其实还有一个被广泛使用的小技巧，该小技巧某种意义上可以说是用到了“动量”的思想：我们会分别维护两个储存“运行均值（Running
Mean）”和“运行方差（Running Variance）”的变量。具体而言：

  1. 输入：某一层在当前 Batch 上的输出、增强数值稳定性所用的小值；动量值（一般取）
  2. 过程：
    首先要初始化 Running Mean、Running Variance 为 0 向量： 并初始化、为 1、0 向量： 然后进行如下操作：
    1. 计算当前 Batch 的均值、方差：
    2. 利用、和动量值更新、：
    3. 利用、规范化处理输出：
    4. 线性变换：
  3. 输出：规范化处理后的输出

最后提三点使用 Normalize 时需要注意的事项：

  • 无论是上述的哪种算法、BN 的训练过程和预测过程的表现都是不同的。具体而言，训练过程和算法中所叙述的一致、均值和方差都是根据当前 Batch 来计算的；但测试过程中的均值和方差不能根据当前 Batch 来计算、而应该根据训练样本集的某些特征来进行计算。对于第二个算法来说，和天然就是很好的、可以用来当测试过程中的均值和方差的变量，对于第一个算法而言就需要额外的计算
  • 对于 Normalize 这个特殊层结构来说、偏置量是一个冗余的变量；这是因为规范化操作（去均值）本身会将偏置量的影响抹去、同时 BN 本身的参数可以说正是破坏对称性的参数，它能比较好地完成原本偏置量所做的工作
  • Normalize 这个层结构是可以加在许多不同地方的（如下图所示的 A、B 和 C 处），原论文将它加在了 A 处、但其实现在很多主流的深层 CNN 结构都将它加在了 C 处；相对而言、加在 B 处的做法则会少一些
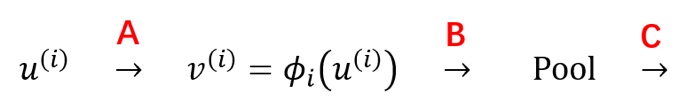
p2.png

在基本了解了 Normalize 对应的 BN 算法之后、我们就可以着手进行实现了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
class Normalize(SubLayer):
    """
        初始化结构
        self._eps：记录增强数值稳定性所用的小值的属性
        self._activation：记录自身的激活函数的属性，主要是为了兼容图7.17 A的情况
        self.tf_rm、self.tf_rv：记录μ_run、σ_run^2的属性
        self.tf_gamma、self.tf_beta：记录γ、β的属性
        self._momentum：记录动量值m的属性
    """
    def __init__(self, parent, shape, activation="Identical", eps=1e-8, momentum=0.9):
        SubLayer.__init__(self, parent, shape)
        self._eps, self._activation = eps, activation
        self.tf_rm = self.tf_rv = None
        self.tf_gamma = tf.Variable(tf.ones(self.shape[1]), name="norm_scale")
        self.tf_beta = tf.Variable(tf.zeros(self.shape[1]), name="norm_beta")
        self._momentum = momentum
        self.description = "(eps: {}, momentum: {})".format(eps, momentum)
    def _activate(self, x, predict):
        # 若μ_run、σ_run^2还未初始化，则根据输入x进行相应的初始化
        if self.tf_rm is None or self.tf_rv is None:
            shape = x.get_shape()[-1]
            self.tf_rm = tf.Variable(tf.zeros(shape), trainable=False, name="norm_mean")
            self.tf_rv = tf.Variable(tf.ones(shape), trainable=False, name="norm_var")
        if not predict:
            # 利用Tensorflow相应函数计算当前Batch的举止、方差
            _sm, _sv = tf.nn.moments(x, list(range(len(x.get_shape()) - 1)))
            _rm = tf.assign(
                self.tf_rm, self._momentum * self.tf_rm + (1 - self._momentum) * _sm)
            _rv = tf.assign(
                self.tf_rv, self._momentum * self.tf_rv + (1 - self._momentum) * _sv)
            # 利用Tensorflow相应函数直接得到Batch Normalization的结果
            with tf.control_dependencies([_rm, _rv]):
                _norm = tf.nn.batch_normalization(
                    x, _sm, _sv, self.tf_beta, self.tf_gamma, self._eps)
        else:
            _norm = tf.nn.batch_normalization(
                x, self.tf_rm, self.tf_rv, self.tf_beta, self.tf_gamma, self._eps)
        # 如果指定了激活函数、就再用相应激活函数作用在BN结果上以得到最终结果
        # 这里只定义了ReLU和Sigmoid两种，如有需要可以很方便地进行拓展
        if self._activation == "ReLU":
            return tf.nn.relu(_norm)
        if self._activation == "Sigmoid":
            return tf.nn.sigmoid(_norm)
        return _norm

重写 CostLayer 结构

在上个系列中，为了整合特殊变换函数和损失函数以更高效地计算梯度、我们花了不少代码来做繁琐的封装；不过由于 Tensorflow 中已经有了这些封装好的、数值性质更优的函数、所以 CostLayer 的实现将会变得非常简单：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
# 定义一个简单的基类
class CostLayer(Layer):
    # 定义一个方法以获取损失值
    def calculate(self, y, y_pred):
        return self._activate(y_pred, y)
# 定义Cross Entropy对应的CostLayer（整合了Softmax变换）
class CrossEntropy(CostLayer):
    def _activate(self, x, y):
        return tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=x, labels=y))
# 定义MSE准则对应的CostLayer
class MSE(CostLayer):
    def _activate(self, x, y):
        return tf.reduce_mean(tf.square(x - y))

短短 15 行代码就实现了上个系列中用 113 行代码才实现的所有功能，由此可窥见 Tensorflow 框架的强大

（话说我这么卖力地安利 Tensorflow，Google 是不是应该给我些广告费什么的）（喂

重写网络结构

由于 Tensorflow 重写的是算法核心部分，作为封装的网络结构其实并不用进行太大的变动；具体而言、整个网络结构需要做比较大的改动的地方只有如下两个：

  • 初始化各个权值矩阵时，从初始化为 Numpy 数组改为初始化为 Tensorflow 数组、同时要注意兼容 CNN 的问题
  • 不用记录所有 Layer 的激活值而只用关心输出 Layer 的输出值和 CostLayer 的损失值（在上个系列中、我们是要记录所有中间结果以进行反向传播算法的）

关于第一点我们会在后面介绍 CNN 的实现时进行说明，这里就仅看看第二点怎么做到：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 定义一个只获取输出Layer的输出值的方法
def _get_rs(self, x, predict=True):
    # 先获取第一层的激活值并用一个 _cache变量进行存储
    _cache = self._layers[0].activate(x, self._tf_weights[0], self._tf_bias[0], predict)
    # 遍历剩余的Layer
    for i, layer in enumerate(self._layers[1:]):
        # 如果到了倒数第二层（输出层）、就进行相应的处理并输出结果
        if i == len(self._layers) - 2:
            # 如果输出层是卷积层、就要把结果铺平
            if isinstance(self._layers[-2], ConvLayer):
                _cache = tf.reshape(_cache, [-1, int(np.prod(_cache.get_shape()[1:]))])
            if self._tf_bias[-1] is not None:
                return tf.matmul(_cache, self._tf_weights[-1]) + self._tf_bias[-1]
            return tf.matmul(_cache, self._tf_weights[-1])
        # 否则、进行相应的前向传导算法
        _cache = layer.activate(_cache, self._tf_weights[i + 1], self._tf_bias[i + 1], predict)

注意：不难看出、get_rs是兼容 CNN 的

有了get_rs这个方法后、Tensorflow 下的网络结构的核心训练步骤就非常简洁了：

1
2
3
4
5
6
# 获取输出值
self._y_pred = self._get_rs(self._tfx, predict=False)
# 利用输出值和CostLayer的calculate方法、计算出损失值
self._cost = self._layers[-1].calculate(self._tfy, self._y_pred)
# 利用Tensorflow帮我们封装的优化器、直接定义出参数的更新步骤
self._train_step = self._optimizer.minimize(self._cost)

完整的、Tensorflow 版本的网络结构的代码可以参见这里，对其深入一些的介绍则在下篇文章的最后一节中进行。此外、我对 Tensorflow 提供的诸多优化器做了一个简单的封装以兼容上个系列实现的优化器的一些接口，具体的代码可以参见这里

观众老爷们能赏个脸么 ( σ'ω')σ