前向传导算法

发表于 | 分类于

时至今日，在各个编程语言的世界里、神经网络的成熟的库都可谓不在少数；这可能就导致有许多人虽然能够熟练应用神经网络、但对于其内部机制却不甚了解。事实上就笔者所展开的简单调查来看，有不少平时经常用到神经网络的程序员其实对神经网络的数学部分有一种“望而生畏”的感觉、其中各种梯度的计算更是让他们发出“眼花缭乱”的感叹

虽然很想说一些令人鼓舞的话，但是如果从繁复性来说、神经网络算法确实是我们目前为止介绍过的算法中推导步骤最多的；不过可以保证的是，如果把算法的逻辑理清，那么静下心来好好演算一下的话、就会觉得它比想象中的简单

算法概述

如果把前文所说过的内容提炼、总结一下的话，就会发现我们其实已经把前向传导算法的过程都叙述了一遍。以一个简单的神经网络结构为例：

一个简单的三层（单隐层）神经网络

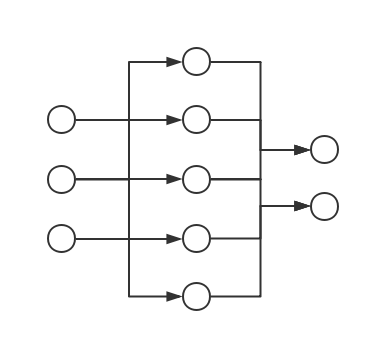
注意：虽然上图将一个个的“节点”画了出来，但是本篇文章及今后的所有讨论中、我们都应该时刻记住：神经网络的基本组成单元是层（Layer）而不是节点，之所以用节点来说明问题也仅仅是为了简化问题、在实现中是需要将节点上的算法“整合”成层的算法的

在展开叙述前、做一些符号约定是有必要的：

  • 记上图中的神经网络从左到右对应的 Layer 为、记中从上往下数的第 j 个神经元为
  • 记对应的：
    • 神经元个数为（从而、、）
    • 激活函数、偏置量分别为、（注意其实不会被用到）
  • 记之间的权值矩阵为、神经元之间的权值为，可知：
  • 记对应的输入、输出为
  • 记模型的输入、输出集为、，样本数为 N，损失函数为；一般我们会要求是一个二元对称函数，亦即对于的输入空间中的任意两个向量（矩阵）、都有：

那么上述神经网络的前向传导算法的所有步骤即为（运算符“”代表矩阵乘法、后同）：

  • 、，注意、都是维矩阵
  • 、，注意是的矩阵、所以、都是维矩阵
  • 、，注意是的矩阵、所以、都是维矩阵

其中即为模型的输出、即为模型在上的损失。可以看到这个过程确实相当平凡、但是里面蕴含的数学思想却是有趣而深刻的，接下来我们就分析一下其中的一些细节

注意：以上这个例子中的神经网络模型其实是一个二分类模型（），如果想用神经网络解决多分类问题（比如 K 分类问题）的话、只需自然地将输出层的神经元个数设为类别个数（）即可。此外，简便起见，如果我们没有特别指出的话、那么下文中所讨论的情况都是、亦即样本集里只有单样本的情形

激活函数

首先说说前文不断在提却又没有细说的激活函数。直观来讲，所谓激活函数、正是整个结构中非线性扭曲力。这里介绍几个常见的激活函数：

逻辑函数（Sigmoid）

其函数图像如下图所示：

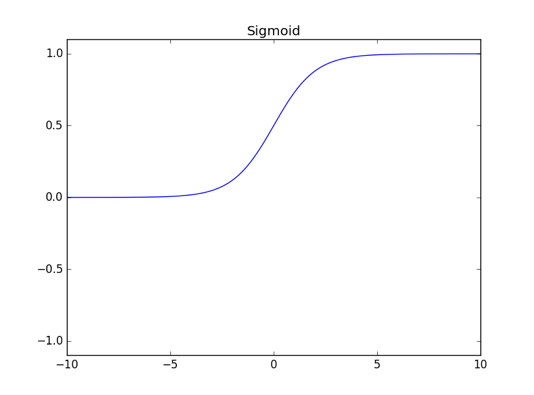
p2.png

正切函数（Tanh）

其函数图像如下图所示：

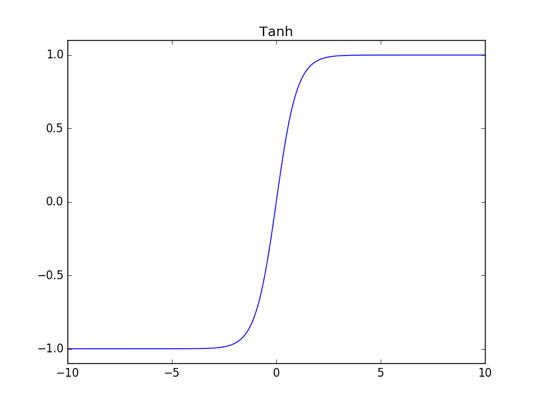
p3.png

线性整流函数（ReLU）

ReLU 的全称是 Rectified Linear Unit，定义式很简洁：

其函数图像如下图所示（注意纵轴范围与上述两个激活函数不同）：

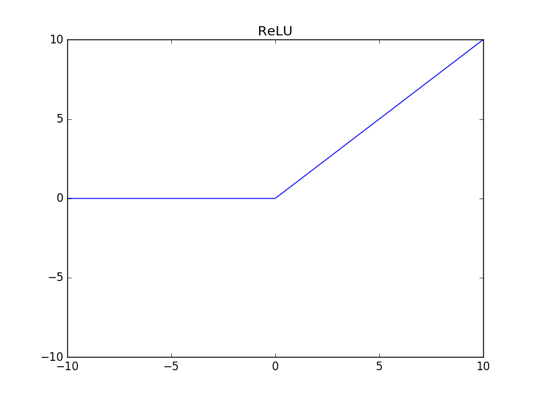
p4.png

ELU 函数（Exponential Linear Unit）

我们在实现时会取、其函数图像如下图所示：

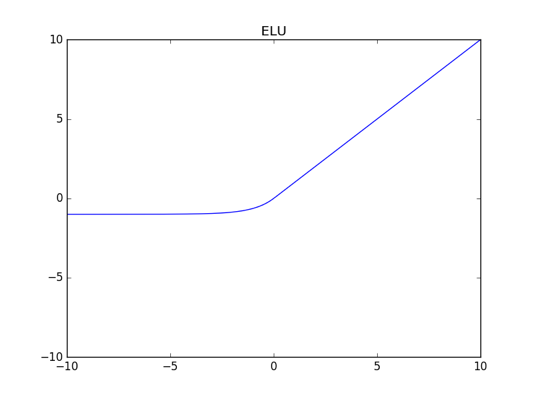
p5.png

Softplus

其函数图像如下图所示：

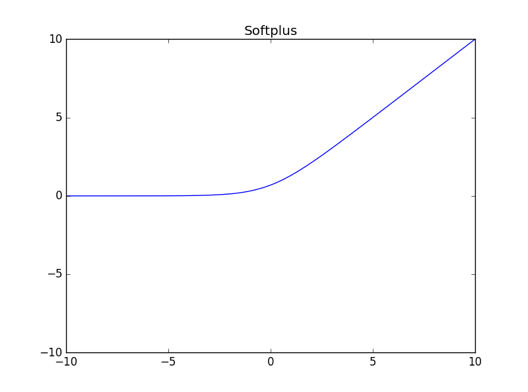
p6.png

恒同映射（Identify）

其函数图像从略

囿于篇幅、这些激活函数的由来及背后相关的错综复杂的数学理论研究就不展开叙述了；我们只需知道，神经网络之所以为非线性模型的关键、其实就在于激活函数

然后来看看层与层之间的权值矩阵以及偏置量、它们的意义也都有比较好的解释：

  • 能把从激活函数得到的函数值线性映射到另一个维度的空间上
  • 能在此基础上再进行一步平移的操作

其中的重要性似乎无需过多说明也能让人明白，但的重要性相对而言可能就没那么明显。为了直观体会偏置量的重要性、可以设想这么一个场景（取之前的三层网络结构来说明问题）：

  • 激活函数全是中心对称的函数（比如常见的 tanh 函数）、亦即：
  • 训练样本集为：
  • 权值矩阵、可变但偏置量恒为 0

在此场景下不难想象，无论我们怎样进行训练、模型在训练集上的准确率都不可能达到 100%。这是因为我们有：

从而由激活函数为中心对称函数可知：

亦即

但我们有、所以模型不可能同时预测对和。事实上由上述讨论可知、此时模型所做的预测必定是关于输入空间“中心对称”的，这当然不是一个良好的结果。而如果我们引入偏置量的话、上述的对称性就会被打破，这就是偏置量重要性的其中一个比较浅显、直观的方面

损失函数（Cost Function）

注意到前向传导算法的最后一步是将模型的输出与真值相比较、并通过损失函数的作用来得到一个损失。损失函数有时也写作 Loss Function、我们之前已经提及它许多次。损失函数的直观意义是明确的：它是模型对数据拟合程度的反映；拟合得越差、损失函数的值就应该越大。如果同时考虑到梯度下降法的应用、我们自然还应该期望，当损失函数在函数值比较大（亦即模型的表现越差）时、它对应的梯度也要比较大（亦即更新参数的幅度也要比较大）

由于我们此前没有对梯度下降法进行过深刻的应用（上个系列中的随机梯度下降只是一个相当粗浅的应用）、所以至今为止我们涉及到的损失函数基本只满足了“模型越差函数值越大”这一点，对于“函数值越大则梯度越大”这一点则没怎么考虑到。而对于神经网络而言、梯度下降可谓就是训练的全部，时至今日也没能出现能够与之抗衡的其余算法、最多也只是不断地研究出各式各样的梯度下降法的变体而已；所以对于神经网络来说，定义一个足够合适的损失函数是有必要的。接下来就介绍其中最常用的几个，为此需要先做符号约定：

  • 假设样本为
  • 假设共有 K 类：
  • 假设讨论的模型为、其输出（向量）为

其中、，且是除了一位为 1、其余位都是 0 的向量。换句话说，若、那么除了第 k 位为 1、其余位都是 0

注意：这种的表示方法通常叫做 one-hot representation

在神经网络的训练算法中、损失函数通常需要结合输出层的激活函数来讨论；不过如果只考虑前向传导算法、只叙述损失函数的基本形式就可以：

  • 距离损失函数 该损失函数对应着最小平方误差准则（Minimum Squared Error，常简称为 MSE），它的直观意义是明确的：模型预测和真值的（欧氏）距离越大、损失就越大，反之就越小
  • 交叉熵损失函数（要求每一位的取值都在中） 其中交叉熵（Cross Entropy）是信息论中的一个概念、其本身是有一定内涵的，感兴趣的观众老爷可以参见维基百科来了解背后的那一套数学理论。囿于篇幅、我们无法展开叙述这一部分，但是从交叉熵的名字就可以看出、它和决策树里面提到过的熵有千丝万缕的关系；考虑到熵是定义在概率分布上的、所以进一步要求是一个概率向量（亦即进一步要求）是一个非常合理的做法
  • log-likelihood 损失函数（要求是一个概率向量、以及不妨假设） 换句话说，log-likelihood 即为模型预测的、真值 y 对应的类（）的概率的负对数。需要指出的是、log-likelihood 这种原始的定义方式在神经网络里面不尽合理，我们会在下一节进行相关的讨论

以上、我们就比较完整地叙述了一遍前向传导算法。可以看出在前向传导算法中、神经网络的各个 Layer 结构在很多地方的表现都一致、所以把 Layer 的共性抽象出来是有必要的。事实上再通过后面对神经网络的训练算法（反向传播算法）的说明我们就可以看出，每个变换层除了所对应的激活函数有所不同以外、其余部分的表现都几乎一样；而 CostLayer 虽然表现会有点不同（比如需要额外考虑损失函数、从而导致反向传播的形式会有些许改变）、其总体结构仍与变换层大致相同

观众老爷们能赏个脸么 ( σ'ω')σ