朴素的网络结构

发表于 | 分类于

这一节主要介绍一下如何进行最简单的封装，对于更加完善的实现则会放在下一节。由于我本人实现的最终版本有上千行，囿于篇幅、无法在这里进行叙述，感兴趣的观众老爷们可以参见这里

总结前文说明过的诸多子结构、不难得知我们用于封装它们的朴素网络结构至少需要实现如下这些功能：

  • 加入一个 Layer
  • 获取各个模型参数对应的优化器
  • 协调各个子结构以实现前向传导算法和反向传播算法

接下来就看看具体的实现。先看其基本框架：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
from f_NN.Layers import *
from f_NN.Optimizers import *
from Util.Bases import
class NaiveNN(ClassifierBase):
    """
        初始化结构
        self._layers、self._weights、self._bias：记录着所有Layer、权值矩阵、偏置量
        self._w_optimizer、self._b_optimizer：记录着所有权值矩阵的和偏置量的优化器
        self._current_dimension：记录着当前最后一个Layer所含的神经元个数
    """
    def __init__(self):
        super(NaiveNN, self).__init__()
        self._layers, self._weights, self._bias = [], [], []
        self._w_optimizer = self._b_optimizer = None
        self._current_dimension = 0

接下来实现加入 Layer 的功能。由于我们只打算进行朴素实现、所以应该对输入模型的 Layer 的格式做出一些限制以减少代码量。具体而言、我们对输入模型的 Layer 做出如下三个约束：

  • 如果该 Layer 是第一次输入模型的 Layer 的话（亦即）、则要求 Layer 的shape属性是一个二元元组，此时shape[0]即为输入数据的维度、shape[1]即为的神经元个数
  • 否则（亦即）、我们要求 Layer 输入模型时的shape属性是一元元组，其唯一的元素记录的就是该Layer的神经元个数

比如说、如果我们想设计含有如下结构的神经网络：

  • 含有一层 ReLU 隐藏层，该层有 24 个神经元
  • 损失函数为 SigmoidCross Entropy 的组合

那么在实现完毕后、需要能够通过如下三行代码：

1
2
3
nn = NaiveNN()
nn.add(ReLU((x.shape[1], 24)))
nn.add(CostLayer((y.shape[1],), "CrossEntropy", transform="Sigmoid"))

来把对应的结构搭建完毕（其中 x、y 是训练集）。以下即为具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def add(self, layer):
    if not self._layers:
        # 如果是第一次加入layer、则初始化相应的属性
        self._layers, self._current_dimension = [layer], layer.shape[1]
        # 调用初始化权值矩阵和偏置量的方法
        self._add_params(layer.shape)
    else:
        _next = layer.shape[0]
        layer.shape = (self._current_dimension, _next)
        # 调用进一步处理Layer的方法
        self._add_layer(layer, self._current_dimension, _next)
def _add_params(self, shape):
    self._weights.append(np.random.randn(*shape))
    self._bias.append(np.zeros((1, shape[1])))
def _add_layer(self, layer, *args):
    _current, _next = args
    self._add_params((_current, _next))
    self._current_dimension = _next
    self._layers.append(layer)

然后就需要获取各个模型参数对应的优化器并实现前向传导算法和反向传播算法了。鉴于我们实现的是朴素的版本、我们只允许用户自定义学习速率、优化器使用的算法及总的迭代次数：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def fit(self, x, y, lr=0.001, optimizer="Adam", epoch=10):
    # 调用相应方法来初始化优化器
    self._init_optimizers(optimizer, lr, epoch)
    layer_width = len(self._layers)
    # 训练的主循环
    # 需要注意的是，在每次迭代中、我们是用训练集中所有样本来进行训练的
    for counter in range(epoch):
        self._w_optimizer.update()
        self._b_optimizer.update()
        # 调用相应方法来进行前向传导算法、把所得的激活值都存储下来
        _activations = self._get_activations(x)
        # 调用CostLayer的bp_first方法来进行BP算法的第一步
        _deltas = [self._layers[-1].bp_first(y, _activations[-1])]
        # BP算法主体
        for i in range(-1, -len(_activations), -1):
            _deltas.append(self._layers[i - 1].bp(
                _activations[i - 1], self._weights[i], _deltas[-1]
            ))
        # 利用各个局部梯度来更新模型参数
        # 注意由于最后一个是CostLayer对应的占位符、所以无需对其更新
        for i in range(layer_width - 1, 0, -1):
            self._opt(i, _activations[i - 1], _deltas[layer_width - i - 1])
        self._opt(0, x, _deltas[-1])

这里用到了三个方法、它们的作用为：

  • self._init_optimizers：根据优化器的名字、学习速率和迭代次数来初始化优化器
  • self._get_activations：进行前向传导算法
  • self._opt：利用局部梯度和优化器来更新模型的各个参数

它们的具体实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def _init_optimizers(self, optimizer, lr, epoch):
    # 利用定义好的优化器工厂来初始化优化器
    # 注意由于最后一层是CostLayer对应的占位符、所以无需把它输进优化器
    _opt_fac = OptFactory()
    self._w_optimizer = _opt_fac.get_optimizer_by_name(
        optimizer, self._weights[:-1], lr, epoch)
    self._b_optimizer = _opt_fac.get_optimizer_by_name(
        optimizer, self._bias[:-1], lr, epoch)
def _get_activations(self, x):
    _activations = [self._layers[0].activate(x, self._weights[0], self._bias[0])]
    for i, layer in enumerate(self._layers[1:]):
        _activations.append(layer.activate(
            _activations[-1], self._weights[i + 1], self._bias[i + 1]))
    return _activations
def _opt(self, i, _activation, _delta):
    self._weights[i] += self._w_optimizer.run(
        i, _activation.T.dot(_delta)
    )
    self._bias[i] += self._b_optimizer.run(
        i, np.sum(_delta, axis=0, keepdims=True)
    )

最后就是模型的预测了，这一部分的实现非常直观易懂：

1
2
3
4
5
6
7
8
9
def predict(self, x, get_raw_results=False):
    y_pred = self._get_prediction(np.atleast_2d(x))
    if get_raw_results:
        return y_pred
    return np.argmax(y_pred, axis=1)
def _get_prediction(self, x):
    # 直接取前向传导算法得到的最后一个激活值即可
    return self._get_activations(x)[-1]

至此、一个朴素的神经网络结构就实现完了；虽说该模型有诸多不足之处，但其基本的框架和模式却都是有普适性的、且它的表现也已经相当不错。可以通过在螺旋线数据集上做几组实验来直观地感受一下这个朴素神经网络的分类能力、结果如下图所示：

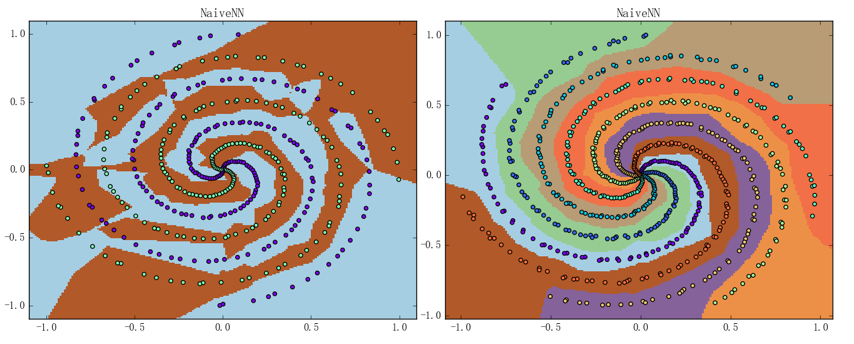
p1.png

左图是 4 条螺旋线的二类分类问题、准确率为 92.75%；右图为 7 条螺旋线的七类分类问题、准确率为 100%；神经网络的结构则都是两层含 24 个神经元的 ReLU 加 SoftmaxCross Entropy 组合的这个结构，迭代次数则为 1000 次、平均训练时间分别为 0.74秒（左图）和 1.04秒（右图）。注意到虽然我们使用的螺旋线数据集的“旋转程度”比之前使用过的螺旋线数据集的都要大不少、但是神经网络的表现仍然相当不错

观众老爷们能赏个脸么 ( σ'ω')σ