参数的更新

发表于 | 分类于

我们之前曾简单地描述过如何使用随机梯度下降来更新参数，本文则主要会介绍一些应用得更多、效果更好的算法。正如上个系列最后所提及的，这些梯度下降的拓展算法从思想上来说和梯度下降法类似、区别则可以简练地概括如下两点：

  • 更新方向不是简单地取为梯度
  • 学习速率不是简单地取为常值

虽然我们不会深入地叙述这些算法背后复杂的数学基础、但我们会对每种算法都提供一些直观的解释。需要指出的是、这些算法都是利用局部梯度来获得一个更好的“梯度”、从而使得“梯度下降”变得更优

具体而言、原始的梯度为：

若想把它向量化、就不得不考虑上训练集中的样本数，此时：

  • 权值矩阵：的维度为
  • 输出向量：的维度为
  • 局部梯度：的维度为

且有

换句话说、原始梯度的向量化形式即为：

而本节所要说明的诸多算法、大多都是利用和其它属性来得到一个比更好的“梯度”、进而把梯度下降从

变成

在接下来的讨论中，我们统一使用代指要更新的参数、用和代指第 t 步迭代中得到的原始梯度和优化后的梯度、用代指学习速率。首先需要指出的是，在众多深度学习的成熟框架中、参数的更新过程常常会被单独抽象成若干个模型，我们常常会称这些模型为“优化器（Optimizer）”。顾名思义、优化器能够根据模型的参数和损失来“优化”模型；具体而言，优化器至少需要能够利用各种算法并根据输入的参数与对应的梯度来进行参数的更新。对于有自身 Graph 结构的深度学习框架而言（比如 Tensorflow），用户甚至只需将参数更新的算法和最终的损失值提供给其优化器、然后该优化器就能够利用 Graph 结构来自动更新各个部分的参数

我们所打算实现的优化器属于最朴素的优化器——根据算法与梯度来更新相应参数；由后文的讨论可知，比较优秀的算法在每一步迭代中计算梯度时都不是独立的、而会利用上以前的计算结果。综上所述、可知优化器的框架应该包括如下三个方法：

  • 接收欲更新的参数并进行相应处理的方法
  • 利用梯度和自身属性来更新参数的方法
  • 在完成参数更新后更新自身属性的方法

尽管一个朴素优化器的实现比较平凡，但对于帮助我们理解各种算法而言还是足够的。考虑到不同算法对应的优化器有许多行为一致的地方，为了合理重复利用代码、我们需要把它们的共性所对应的实现抽象出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np
class Optimizer:
    """
        初始化结构
        self.lr：记录学习速率的参数，默认为0.01
        self._cache：储存中间结果的参数，在不同算法中的表现会不同
    """
    def __init__(self, lr=0.01, cache=None):
        self.lr = lr
        self._cache = cache
    def __str__(self):
        return self.__class__.__name__
    def __repr__(self):
        return str(self)
    # 接收欲更新的参数并进行相应处理，注意有可能传入多个参数
    # 默认行为是创建若干个和传入的各个参数形状相等的0矩阵并把它们存在self._cache中
    def feed_variables(self, variables):
        self._cache = [
            np.zeros(var.shape) for var in variables
        ]
    # 利用负梯度和优化器自身的属性来返回最终更新步伐的方法
    # 注意这里的i是指优化器中的第i个参数
    def run(self, i, dw):
        pass
    # 完成参数更新后、更新自身属性的方法
    def update(self):
        pass

接下来就看看各种常用的参数更新算法的说明和相应实现

Vanilla Update

Vanilla 在机器学习中常用来表示“朴实的”、“平凡的”，换句话说、Vanilla
Update 和最普通的梯度下降法别无二致，亦即：

在实际实现中、Vanilla Update 通常以小批量梯度下降法（MBGD）的形式出现：

1
2
3
class MBGD(Optimizer):
    def run(self, i, dw):
        return self.lr * dw

其中通常会是一个矩阵（对应 MBGD 算法）而非一个数（对应 SGD 算法）。

注意：即使是 SGD、其实也属于 Vanilla Update

Momentum Update

Vanilla Update 的缺点是比较明显的：以 MBGD 为例，它每一步迭代中参数的更新是完全独立的、亦即第t步参数的更新方向只依赖于当前所用的 batch，这在物理意义上是不太符合直观的。可以进行如下设想：

  • 将损失函数的图像想象成一个山谷、我们的目的是达到谷底
  • 将损失函数某一点的梯度想象成该点对应的坡度
  • 将学习速率想象成沿坡度行走的速度

如果是 Vanilla Update 的话，就相当于可能会出现明明前一秒还在以很快的速度往左走、这一秒就突然开始以很快的速度往右走。这种“行进模式”之所以违背直观、是因为没有考虑到我们都很熟悉的“惯性”。Momentum Update 正是通过尝试模拟物体运动时的“惯性”以期望增加算法收敛的速度和稳定性，其优化公式为：

其中梯度的物理意义即为“动力”、的物理意义即为第 t 步迭代中参数的“行进速度”、的物理意义即为惯性，它描述了上一步的行进速度会在多大程度上影响到这一步的行进速度。易知当时、Momentum Update等价于 Vanilla Update

一般来说我们不会把设置为一个常量、而会把它设置成一个会随训练过程的推进而变动的变量；同时一般来说、我们会将的初始值设为 0.5 并逐步将它加大至 0.99。该做法蕴含着如下两个思想：

  • 认为训练刚开始时的梯度会比较大而训练后期时梯度会变小，通过逐步调大、我们能够使更新的步伐一直保持在比较大的水平
  • 认为当我们接近谷底时、我们应该尽量减少“动力”带来的影响而保持原有的方向前进。这是因为如果每一步都直接往谷底方向走（亦即运动仅受动力影响）的话、就会很容易由于动力大小难以拿捏而引发震荡

该做法所对应的实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class Momentum(Optimizer, metaclass=TimingMeta):
    """
        初始化结构（Momentum Update版本）
        self._momentum：记录“惯性”的属性
        self._step：每一步迭代后“惯性”的增量
        self._floor、self._ceiling：“惯性”的最小、最大值
        self._cache：对于Momentum Update而言、该属性记录的就是“行进速度”
        self._is_nesterov：处理Nesterov Momentum Update的属性，这里暂时按下不表
    """
    def __init__(self, lr=0.01, cache=None, epoch=100, floor=0.5, ceiling=0.999):
        Optimizer.__init__(self, lr, cache)
        self._momentum = floor
        self._step = (ceiling - floor) / epoch
        self._floor, self._ceiling = floor, ceiling
        self._is_nesterov = False
    def run(self, i, dw):
        dw *= self.lr
        velocity = self._cache
        velocity[i] *= self._momentum
        velocity[i] += dw
        return velocity[i]
    def update(self):
        if self._momentum < self._ceiling:
            self._momentum += self._step

当然也不是说只能用这种方法来调整的值，对于一些特殊的情况、确实是会有更好且更具针对性的更新策略的

Nesterov Momentum Update

从名字不难想象，Nesterov Momentum Update 方法是基于 Momentum Update 方法的，它由 Ilya Sutskever 在 Nesterov 相关工作（Nesterov Accelerated Gradient，常简称为 NAG）的启发下提出。它在凸优化问题下的收敛性会比传统的 Momentum Update 要更好，而在实际任务中它也确实经常表现得更优

Nesterov Momentum Update 的核心思想在于想让算法具有“前瞻性”。简单来说、它会利用“下一步”的梯度而不是“这一步”的梯度来合成出最终的更新步伐（所谓更新步伐、可以直观地理解为“更新方向更新幅度”）。可以通过下图来直观地认知这个过程：

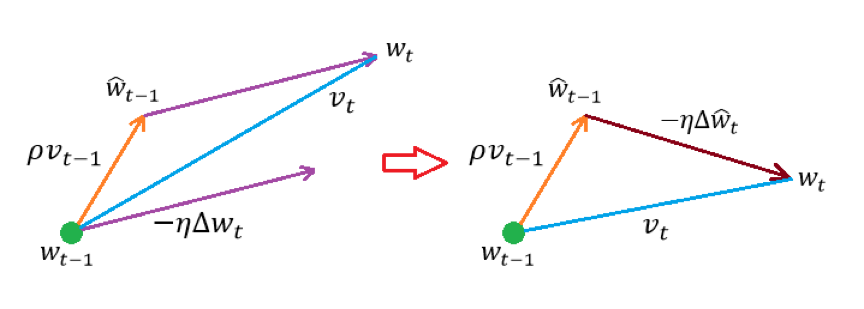
p1.png

左图为普通的 Momentum Update、经由如下两部分合成而得：

  • 起点处的行进速度
  • 中继点处的更新步伐（处的负梯度与学习速率的乘积）

右图则为 Nesterov Momentum Update、经由如下两部分合成而得：

  • 起点处的行进速度
  • 中继点处的更新步伐（处的负梯度与学习速率的乘积）

于是不难写出 Nesterov Momentum Update 的优化公式：

但是这里的计算却不是一个平凡的问题。对此、Yoshua Bengio 等人在论文《Advances In Optimizing Recurrent Networks》里面提出了一个利用到换参法的解决方案。具体而言、令：

注意到

从而

综上所述、不难得到换参后的优化公式：

可以看出该更新公式和 Momentum Update 中的更新公式非常类似、从而在实现层面上也基本相同。事实上、只需将 Momentum 优化器中的run方法改写为：

1
2
3
4
5
6
7
8
9
10
def run(self, i, dw):
    dw *= self.lr
    velocity = self._cache
    velocity[i] *= self._momentum
    velocity[i] += dw
    # 如果不是Nesterov Momentum Update、可以直接把当成更新步伐
    if not self._is_nesterov:
        return velocity[i]
    # 否则、调用公式来计算更新步伐
    return self._momentum * velocity[i] + dw

然后再让 Nesterov Momentum Update 对应的优化器（NAG 优化器）继承 Momentum 优化器、并把self._is_nesterov这项属性设为 True 即可：

1
2
3
4
class NAG(Momentum):
    def __init__(self, lr=0.01, cache=None, epoch=100, floor=0.5, ceiling=0.999):
        Momentum.__init__(self, lr, cache, epoch, floor, ceiling)
        self._is_nesterov = True

RMSProp

RMSProp 方法与 Momentum 系的方法最根本的不同在于：Momentum 系算法是通过搜索更优的更新方向来进行优化、而 RMSProp 则是通过实时调整学习速率来进行优化。具体而言、它的优化公式为：

其中有两个变量是需要注意的：

  • 中间变量，它是从算法开始到当前步骤的所有梯度的某种“累积”
  • 衰减系数，它反映了比较早的梯度对当前梯度的影响、越小则影响越小

换句话说、在 RMSProp 算法中，“累积”的梯度越小会导致当前更新步伐越大、反之则会越小。关于这种做法的合理性有许多种解释，我可以提供一个仅供参考的说法：如果徘徊回了原点自然需要奋发图强地开辟新天地、如果已经走了很远自然应该谨小慎微（？？？）

值得一提的是，RMSProp 其实可以算是 AdaGrad（Adaptive Gradient）方法的改进；深入的讨论会牵扯到许多数学理论、这里就只看看应该怎样实现它：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
class RMSProp(Optimizer):
    """
        初始化结构（RMSProp版本）
        self.decay_rate：记录的属性，一般会取0.9、0.99或0.999
        self.eps：算法的平滑项、用于增强算法稳定性，通常取中的某个数
        self._cache：对于RMSProp而言、该属性记录的就是中间变量
    """
    def __init__(self, lr=0.01, cache=None, decay_rate=0.9, eps=1e-8):
        Optimizer.__init__(self, lr, cache)
        self.decay_rate, self.eps = decay_rate, eps
    def run(self, i, dw):
        self._cache[i] = self._cache[i] * self.decay_rate + (1 - self.decay_rate) * dw ** 2
        return self.lr * dw / (np.sqrt(self._cache[i] + self.eps))

Adam

Adam 算法是应用最广泛的、一般而言效果最好的算法，它高效、稳定、适用于绝大多数的应用场景。一般来说如果不知道该选哪种优化算法的话、使用Adam常常会是个不错的选择。它的数学理论背景是相当复杂的、这里就只写出它的一个简化版的优化公式：

从直观上来说、Adam 算法很像是 Momentum 系算法和 RMSProp 算法的结合（中间变量的相关计算类似于 Momentum 系算法对更新方向的选取、中间变量的相关计算则类似于 RMSProp 算法对学习速率的调整）。同样的、我们跳过其背后的那一套数学理论并仅说明如何进行实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
class Adam(Optimizer):
    """
        初始化结构（Adam版本）
        self.beta1、self.beta2：记录、的属性，一般会取、
        self.eps：意义与RMSProp中的eps一致、常取
        self._cache：对于Adam而言、该属性记录的就是中间变量和中间变量
    """
    def __init__(self, lr=0.01, cache=None, beta1=0.9, beta2=0.999, eps=1e-8):
        Optimizer.__init__(self, lr, cache)
        self.beta1, self.beta2, self.eps = beta1, beta2, eps
    def feed_variables(self, variables):
        self._cache = [
            [np.zeros(var.shape) for var in variables],
            [np.zeros(var.shape) for var in variables],
        ]
    def run(self, i, dw):
        self._cache[0][i] = self._cache[0][i] * self.beta1 + (1 - self.beta1) * dw
        self._cache[1][i] = self._cache[1][i] * self.beta2 + (1 - self.beta2) * (dw ** 2)
        return self.lr * self._cache[0][i] / (np.sqrt(self._cache[1][i] + self.eps))

Factory

前 5 小节分别介绍了 5 种常用的优化算法及对应的优化器的实现、这一小节主要介绍的就是如何应用这些实现好的优化器。虽说直接对它们进行调用也无不可，但是考虑到编程中的一些“套路”、我们可以实现一个简单的工厂来“生产”这些优化器：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class OptFactory:
    # 将所有能用的优化器存进一个字典
    available_optimizers = {
        "MBGD": MBGD,
        "Momentum": Momentum, "NAG": NAG,
        "RMSProp": RMSProp, "Adam": Adam,
    }
    # 定义一个能通过优化器名字来获取优化器的方法
    def get_optimizer_by_name(self, name, variables, lr, epoch):
        try:
            _optimizer = self.available_optimizers[name](lr)
            if variables is not None:
                _optimizer.feed_variables(variables)
            if epoch is not None and isinstance(_optimizer, Momentum):
                _optimizer.epoch = epoch
            return _optimizer

至此、我们就对如何更新神经网络中的参数进行了比较全面的说明；结合上一节所实现的 Layer 结构、我们接下来要做的事情就很明确了：定义一个总的框架、把 Layer、Optimizer 有机地结合在一起、从而得到最终能用的 NN 模型

观众老爷们能赏个脸么 ( σ'ω')σ