本文会叙述之前没有解决的纯数学问题,虽然它们仅会涉及到求导相关的知识、但是仍然具有一定难度
BP 算法的推导
要想知道 BP 算法的推导,我们需要且仅需要知道两点知识:求导及其链式法则。由前文的诸多说明可知、我们至少需要知道如下几件事:
- 梯度是向量函数在某点上升最快的方向、其数学定义为 它是向量函数对 n 个分量的偏导组成的向量。需要指出的是,我个人的习惯是在推导向量函数的梯度时,先把它分拆成单个的函数进行普通函数的求偏导计算、最后再把它们合成梯度。后文的推导也会采取这种形式
- BP 算法的初始输入是真实的类别向量
- 我们的目标是让模型的输出尽可能拟合。为此我们会定义:
- 预测函数,它是一个向量函数、会根据输入矩阵输出预测向量
- 损失函数,它是一个标量函数、其函数值能反映和的差异;差异越大、的值就越大
接下来就可以进行具体的推导了。如前所述,我们会把求解梯度的过程化为若干个求解偏导数的问题、然后再把结果进行整合;换句话说,我们会先以单个的神经元为基本单元进行分析、然后再把神经元上的结果整合成 Layer 上的结果
先来通过下图来进行一些符号约定:
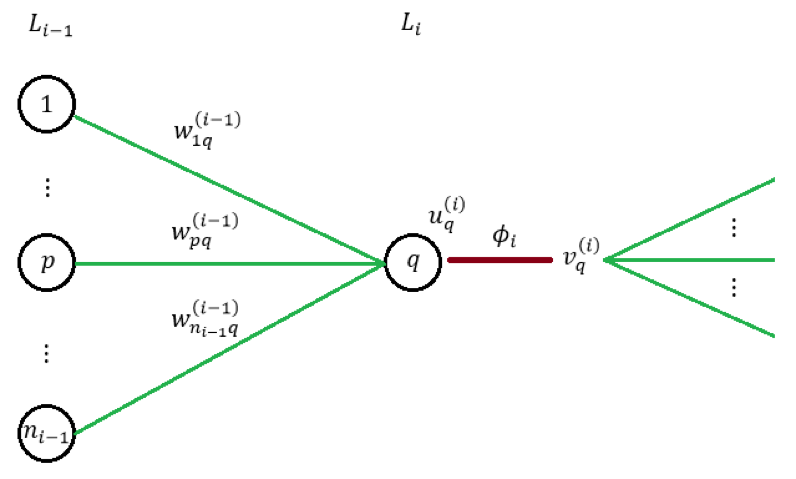
其中
代表着第 k 层第 j 个神经元接收的输入;
代表着对应的激活值。注意我们在前文已经说过、局部梯度的定义可以写为
接下来我们尝试把它转化成 BP 算法中相应的公式。首先由链式法直接可得:
这就可以直接导出最朴素的 SGD 算法。继续往下推导的话会遇到两种情况:
- 当前 Layer 是 CostLayer、也就是说最后一层,此时有: 相当长的式子、里面涉及到的定义也挺多,不过其实每一步的本质都只是链式法则而已。注意最后出现了一项,它其实是输出层激活函数对应的导函数
- 当前 Layer 不是最后一层时,同样由链式法则可知(注意:该层的每个神经元对下一层所有神经元都会有影响) 其中 即为下一层传播回来的局部梯度;且由于 从而可知
以上就是所有的推导过程,将结果进行整合之后、不难得出前文出现过的这些公式:
- 对 CostLayer 而言、有
- 对其余 Layer 而言、有
Softmaxlog-likelihood 组合
这一节主要说明下常见组合——Softmaxlog-likelihood 的梯度公式的推导,不过在此之前可能需要复习一下符号约定:
- 假设输入为、输出为
- 假设模型在 Softmax 之前的输出为
- 假设模型的 Softmax 接受的输入为
- 假设模型在 Softmax 之后的输出为 其中
- 假设模型的损失为 log-likelihood:
接下来开始正式的推导。同样先以神经元为基本单位进行分析、可知:
注意到
所以我们只需要考虑的情况、此时有
注意到
以及
故
综上所述、即得
亦即
若将 log-likelihood 改进为
即得

