MultinomialNB 的实现

发表于 | 分类于

（本文会用到的所有代码都在这里）

本文主要介绍离散型朴素贝叶斯——MultinomialNB 的实现。对于离散型朴素贝叶斯模型的实现，由于核心算法都是在进行“计数”工作、所以问题的关键就转换为了如何进行计数。幸运的是、Numpy 中的一个方法：bincount就是专门用来计数的，它能够非常快速地数出一个数组中各个数字出现的频率；而且由于它是 Numpy 自带的方法，其速度比 Python 标准库collections中的计数器Counter还要快上非常多。不幸的是、该方法有如下两个缺点：

  • 只能处理非负整数型中数组
  • 向量中的最大值即为返回的数组的长度，换句话说，如果用bincount方法对一个长度为 1、元素为 1000 的数组计数的话，返回的结果就是 999 个 0 加 1 个 1

所以我们做数据预处理时就要充分考虑到这两点

在综述中我们曾经提到过在这里可以找到将数据进行数值化的具体实现，该数据数值化的方法其实可以说是为bincount方法“量身定做”的。举个栗子，当原始数据形如：

1
2
3
4
5
x, s, n, t, p, f
x, s, y, t, a, f
b, s, w, t, l, f
x, y, w, t, p, f
x, s, g, f, n, f

时，调用上述数值化数据的方法将会把数据数值化为：

1
2
3
4
5
0, 0, 0, 0, 0, 0
0, 0, 1, 0, 1, 0
1, 0, 2, 0, 2, 0
0, 1, 2, 0, 0, 0
0, 0, 3, 1, 3, 0

单就实现这个功能而言、实现是平凡的：

1
2
3
4
5
6
7
8
9
def quantize_data(x):
    features = [set(feat) for feat in xt]
    feat_dics = [{
        _l: i for i, _l in enumerate(feats)
    } if not wc[i] else None for i, feats in enumerate(features)]
    x = np.array([[
        feat_dics[i][_l] for i, _l in enumerate(sample)]
            for sample in x])
    return x, feat_dics

不过考虑到离散型朴素贝叶斯需要的东西比这要多很多，所以才有了这里所实现的、相对而言繁复很多的版本。建议观众老爷们在看接下来的实现之前先把那个quantize_data函数的完整版看一遍、因为我接下来会直接用（那你很棒棒哦）

当然，考虑到朴素贝叶斯的相关理论还是比较多的、我就不把实现一股脑扔出来了，那样估计大部分人（包括我自己在内）都看不懂……所以我决定把离散型朴素贝叶斯算法和对应的实现进行逐一讲解 ( σ’ω’)σ

计算先验概率

这倒是在将框架时就已经讲过了、但我还是打算重讲一遍以加深理解。首先把实现放出来：

1
2
3
def get_prior_probability(self, lb=1):
    return [(_c_num + lb) / (len(self._y) + lb * len(self._cat_counter))
        for _c_num in self._cat_counter]

其中的lb为平滑系数（默认为 1、亦即拉普拉斯平滑），这对应的公式其实是带平滑项的、先验概率的极大似然估计：

所以代码中的self._cat_counter的意义就很明确了——它存储着 K 个

（cat counter 是 category counter 的简称）（我知道我命名很差所以不要打我）

计算条件概率

同样先看核心实现：

1
2
3
4
5
6
7
data = [[] for _ in range(n_dim)]
for dim, n_possibilities in enumerate(self._n_possibilities):
    data[dim] = [[
        (self._con_counter[dim][c][p] + lb) / (
            self._cat_counter[c] + lb * n_possibilities)
        for p in range(n_possibilities)] for c in range(n_category)]
self._data = [np.array(dim_info) for dim_info in data]

这对应的公式其实就是带平滑项（lb）的条件概率的极大似然估计：

其中

可以看到我们利用到了self._cat_counter属性来计算。同时可以看出：

  • n_category即为 K
  • self._n_possibilities储存着 n 个
  • self._con_counter储存的即是各个的值。具体而言：

至于self._data、就只是为了向量化算法而存在的一个变量而已，它将data中的每一个列表都转成了 Numpy 数组、以便在计算后验概率时利用 Numpy 数组的 Fancy Indexing 来加速算法

聪明的观众老爷可能已经发现、其实self._con_counter才是计算条件概率的关键，事实上这里也正是bincount大放异彩的地方。以下为计算self._con_counter的函数的实现：

1
2
3
4
5
6
7
8
9
10
11
12
def feed_sample_weight(self, sample_weight=None):
    self._con_counter = []
    for dim, _p in enumerate(self._n_possibilities):
        if sample_weight is None:
            self._con_counter.append([
                np.bincount(xx[dim], minlength=_p) for xx in
                    self._labelled_x])
        else:
            self._con_counter.append([
                np.bincount(xx[dim], weights=sample_weight[
                    label] / sample_weight[label].mean(), minlength=_p)
                for label, xx in self._label_zip])

可以看到、bincount方法甚至能帮我们处理样本权重的问题

代码中有两个我们还没进行说明的属性：self._labelled_x和self._label_zip，不过从代码上下文不难推断出、它们储存的是应该是不同类别所对应的数据。具体而言：

  • self._labelled_x：记录按类别分开后的、输入数据的数组
  • self._label_zip：比self._labelled_x多记录了个各个类别的数据所对应的下标

这里就提前将它们的实现放出来以帮助理解吧：

1
2
3
4
5
# 获得各类别数据的下标
labels = [y == value for value in range(len(cat_counter))]
# 利用下标获取记录按类别分开后的输入数据的数组
labelled_x = [x[ci].T for ci in labels]
self._labelled_x, self._label_zip = labelled_x, list(zip(labels, labelled_x))

计算后验概率

仍然先看核心实现：

1
2
3
4
5
6
def func(input_x, tar_category):
    input_x = np.atleast_2d(input_x).T
    rs = np.ones(input_x.shape[1])
    for d, xx in enumerate(input_x):
        rs *= self._data[d][tar_category][xx]
    return rs * p_category[tar_category]

这对应的公式其实就是决策公式：

所以不难看出代码中的p_category存储着 K 个

整合封装模型

最后要做的、无非就是把上述三个步骤进行封装而已，首先是数据预处理：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def feed_data(self, x, y, sample_weight=None):
    if sample_weight is not None:
        sample_weight = np.array(sample_weight)
    # 调用 quantize_data 函数获得诸多信息
    x, y, _, features, feat_dics, label_dic = DataUtil.quantize_data(
        x, y, wc=np.array([False] * len(x[0])))
    # 利用 bincount 函数直接获得 self._cat_counter
    cat_counter = np.bincount(y)
    # 利用 features 变量获取各个维度的特征个数 Sj
    n_possibilities = [len(feats) for feats in features]
    # 获得各类别数据的下标
    labels = [y == value for value in range(len(cat_counter))]
    # 利用下标获取记录按类别分开后的输入数据的数组
    labelled_x = [x[ci].T for ci in labels]
    # 更新模型的各个属性
    self._x, self._y = x, y
    self._labelled_x, self._label_zip = labelled_x, list(
        zip(labels, labelled_x))
    self._cat_counter, self._feat_dics, self._n_possibilities = cat_counter, feat_dics, n_possibilities
    self.label_dic = label_dic
    self.feed_sample_weight(sample_weight)

然后利用上一章我们定义的框架的话、只需定义核心训练函数即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
def _fit(self, lb):
    n_dim = len(self._n_possibilities)
    n_category = len(self._cat_counter)
    p_category = self.get_prior_probability(lb)
    data = [[] for _ in range(n_dim)]
    for dim, n_possibilities in enumerate(self._n_possibilities):
        data[dim] = [[
            (self._con_counter[dim][c][p] + lb) / (
                self._cat_counter[c] + lb * n_possibilities)
            for p in range(n_possibilities)] for c in range(n_category)]
    self._data = [np.array(dim_info) for dim_info in data]
    def func(input_x, tar_category):
        input_x = np.atleast_2d(input_x).T
        rs = np.ones(input_x.shape[1])
        for d, xx in enumerate(input_x):
            rs *= self._data[d][tar_category][xx]
        return rs * p_category[tar_category]
    return func

最后，我们需要定义一个将测试数据转化为模型所需的、数值化数据的方法：

1
2
3
4
5
def _transfer_x(self, x):
    for i, sample in enumerate(x):
        for j, char in enumerate(sample):
            x[i][j] = self._feat_dics[j][char]
    return x

至此，离散型朴素贝叶斯就全部实现完毕了（鼓掌！）

评估与可视化

我们可以先拿之前的气球数据集 1.0、1.5 来简单地评估一下我们的模型。首先我们要定义一个能够将文件中的数据转化为 Python 数组的类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class DataUtil:
    # 定义一个方法使其能从文件中读取数据
    # 该方法接受五个参数：
        数据集的名字、数据集的路径、训练样本数、类别所在列、是否打乱数据
    def get_dataset(name, path, train_num=None, tar_idx=None, shuffle=True):
        x = []
        # 将编码设为utf8以便读入中文等特殊字符
        with open(path, "r", encoding="utf8") as file:
            # 如果是气球数据集的话、直接依逗号分割数据即可
            if "balloon" in name:
                for sample in file:
                    x.append(sample.strip().split(","))
        # 默认打乱数据
        if shuffle:
            np.random.shuffle(x)
        # 默认类别在最后一列
        tar_idx = -1 if tar_idx is None else tar_idx
        y = np.array([xx.pop(tar_idx) for xx in x])
        x = np.array(x)
        # 默认全都是训练样本
        if train_num is None:
            return x, y
        # 若传入了训练样本数，则依之将数据集切分为训练集和测试集
        return (x[:train_num], y[:train_num]), (x[train_num:], y[train_num:])

需要指出的是，今后获取各种数据的过程都会放在上述DataUtil中的这个get_dataset方法中，其完整版本可以参见这里。下面就放出 MultinomialNB 的评估用代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
if __name__ == '__main__':
    # 导入标准库time以计时，导入DataUtil类以获取数据
    import time
    from Util import DataUtil
    # 遍历1.0、1.5两个版本的气球数据集
    for dataset in ("balloon1.0", "balloon1.5"):
        # 读入数据
        _x, _y = DataUtil.get_dataset(dataset, "../../_Data/{}.txt".format(dataset))
        # 实例化模型并进行训练、同时记录整个过程花费的时间
        learning_time = time.time()
        nb = MultinomialNB()
        nb.fit(_x, _y)
        learning_time = time.time() - learning_time
        # 评估模型的表现，同时记录评估过程花费的时间
        estimation_time = time.time()
        nb.evaluate(_x, _y)
        estimation_time = time.time() - estimation_time
        # 将记录下来的耗时输出
        print(
            "Model building  : {:12.6} s\n"
            "Estimation      : {:12.6} s\n"
            "Total           : {:12.6} s".format(
                learning_time, estimation_time,
                learning_time + estimation_time
            )
        )

上面这段代码的运行结果如下图所示：

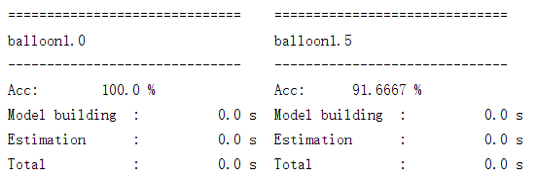
p4.png

由于数据量太少、所以建模和评估的过程耗费的时间已是可以忽略不计的程度。同时正如前文所提及的，气球数据集1.5是“不太均衡”的数据集，所以朴素贝叶斯在其上的表现会比较差

仅仅在虚构的数据集上进行评估可能不太有说服力，我们可以拿 UCI 上一个比较出名（简单）的“蘑菇数据集（Mushroom Data Set）”来评估一下我们的模型。该数据集的大致描述如下：它有 8124 个样本、22 个属性，类别取值有两个：“能吃”或“有毒”；该数据每个单一样本都占一行、属性之间使用逗号隔开。选择该数据集的原因是它无需进行额外的数据预处理、样本量和属性量都相对合适、二类分类问题也相对来说具有代表性。更重要的是，它所有维度的特征取值都是离散的、从而非常适合用来测试我们的 MultinomialNB 模型

完整的数据集可以参见这里（第一列数据是类别），我们的模型在其上的表现则如下图所示：

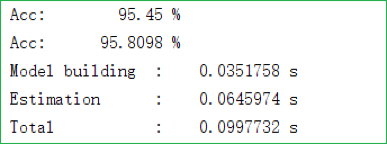
p1.png

其中第一、二行分别是训练集、测试集上的准确率，接下来三行则分别是建立模型、评估模型和总花费时间的记录

当然，仅仅看一个结果没有什么意思、也完全无法知道模型到底干了什么。为了获得更好的直观，我们可以进行一定的可视化，比如说将极大似然估计法得到的条件概率画出（如综述所示的那样）。可视化的代码实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 导入 matplotlib 库以进行可视化
import matplotlib.pyplot as plt
# 进行一些设置使得 matplotlib 能够显示中文
from pylab import mpl
# 将字体设为“仿宋”
mpl.rcParams['font.sans-serif'] = ['FangSong']
mpl.rcParams['axes.unicode_minus'] = False
# 利用 MultinomialNB 搭建过程中记录的变量获取条件概率
data = nb["data"]
# 定义颜色字典，将类别 e（能吃）设为天蓝色、类别 p（有毒）设为橙色
colors = {"e": "lightSkyBlue", "p": "orange"}
# 利用转换字典定义其“反字典”，后面可视化会用上
_rev_feat_dics = [{_val: _key for _key, _val in _feat_dic.items()} 
    for _feat_dic in self._feat_dics]
# 遍历各维度进行可视化
# 利用 MultinomialNB 搭建过程中记录的变量，获取画图所需的信息
for _j in range(nb["x"].shape[1]):
    sj = nb["n_possibilities"][_j]
    tmp_x = np.arange(1, sj+1)
    # 利用 matplotlib 对 LaTeX 的支持来写标题，两个 $ 之间的即是 LaTeX 语句
    title = "$j = {}; S_j = {}$".format(_j+1, sj)
    plt.figure()
    plt.title(title)
    # 根据条件概率的大小画出柱状图
    for _c in range(len(nb.label_dic)):
        plt.bar(tmp_x-0.35*_c, data[_j][_c, :], width=0.35,
                facecolor=colors[nb.label_dic[_c]], edgecolor="white", 
                label="class: {}".format(nb.label_dic[_c]))
    # 利用上文定义的“反字典”将横坐标转换成特征的各个取值
    plt.xticks([i for i in range(sj + 2)], [""] + [_rev_dic[i] for i in range(sj)] + [""])
    plt.ylim(0, 1.0)
    plt.legend()
    # 保存画好的图像
    plt.savefig("d{}".format(j+1))

由于蘑菇数据一共有 22 维，所以上述代码会生成 22 张图，从这些图可以非常清晰地看出训练数据集各维度特征的分布。下选出几组有代表性的图片进行说明

一般来说，一组数据特征中会有相对“重要”的特征和相对“无足轻重”的特征，通过以上实现的可视化可以比较轻松地辨析出在离散型朴素贝叶斯中这两者的区别。比如说，在离散型朴素贝叶斯里、相对重要的特征的表现会如下图所示（左图对应第 5 维、右图对应第 19 维）：

“优秀”的特征

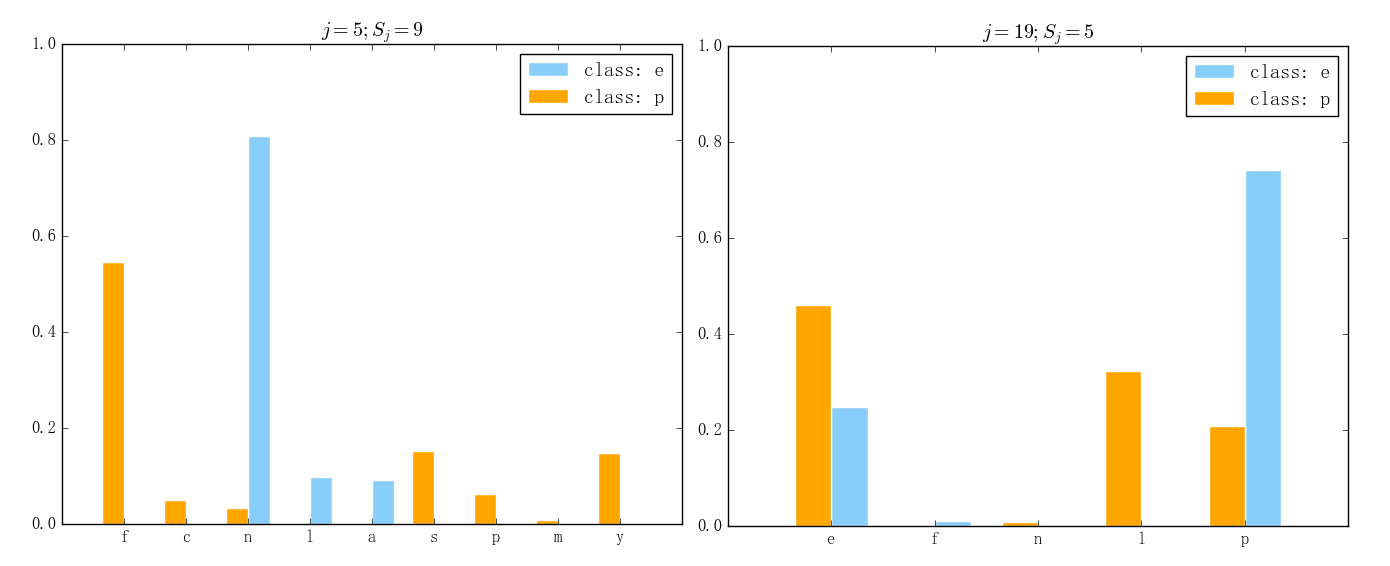
可以看出，蘑菇数据集在第 19 维上两个类别各自的“优势特征”都非常明显、第 5 维上两个类别各自特征的取值更是基本没有交集。可以想象，即使只根据第 5 维的取值来进行类别的判定、最后的准确率也一定会非常高

那么与之相反的、在 MultinomialNB 中相对没那么重要的特征的表现则会形如下图所示（左图对应第 3 维、右图对应第 16 维）：

“无用”的特征

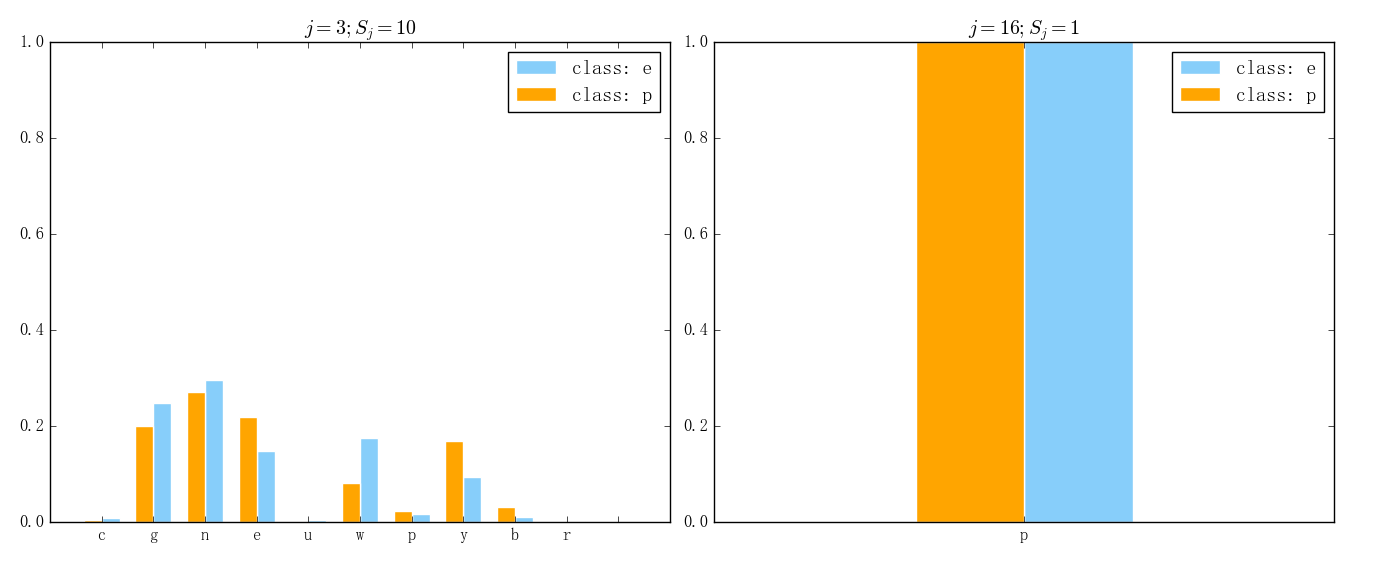
可以看出，蘑菇数据集在第 3 维上两个类的特征取值基本没有什么差异、第 16 维数据更是似乎完全没有存在的价值。像这样的数据就可以考虑直接剔除掉

看到这里的观众老爷如果再回过头去看上一篇文章所讲的框架、想必会有些新的体会吧 ( σ’ω’)σ

观众老爷们能赏个脸么 ( σ'ω')σ