从名字也可以看出、卷积神经网络（CNN）其实是神经网络（NN）的一种拓展，而事实上从结构上来说，朴素的 CNN 和朴素的 NN 没有任何区别（当然，引入了特殊结构的、复杂的 CNN 会和 NN 有着比较大的区别）。本文主要会说一下 CNN 的思想以及它到底在 NN 的基础上做了哪些改进，同时也会说一下 CNN 能够解决的任务类型

“视野”的共享

CNN 的主要思想可以概括为如下两点：

局部连接（Sparse Connectivity）
权值共享（Shared Weights）

它们具有很好的直观。举一个从学术上可能不太严谨的例子：我们平时看风景时，由于视野有限、我们通常并不能将整个风景收入眼中；取而代之、我们每次只能接受视野中的、整个风景的一块“局部风景”（所谓的【局部感受野】）。如果想要欣赏整个风景的话、我们就会不断地“四处张望”。在这个过程中，我们的思想在看的过程中通常是不怎么变的；而在看完后可能整合该过程中所有视野所看到的“局部风景”并发出“这风景真美”的感慨、然后可能会根据这个感慨来调整我们的思想。在这个例子中，我们的视野就可以看作所谓的“局部连接”，我们的思想则可以看作是“共享的权值”（注：这个栗子是我开脑洞开出来的、完全不能保证其学术严谨性、还请各位观众老爷们带着批判的眼光去看待它……如果有这方面专长的观众老爷发现我完全就在瞎扯淡、还望不吝指出 ( σ’ω’)σ）

光用文字叙述可能还是有些懵懂，我来画张图（参考了一张被引用烂了的图；但由于原图有一定的误导性、所以还是打算自己画一个）（虽然很丑）：

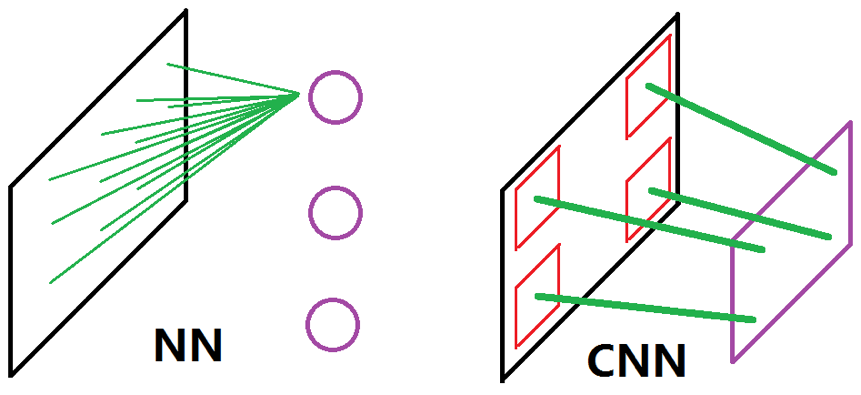
这张图比较了 NN 和 CNN 的思想差别。左图为 NN，可以看到它在处理输入时是全连接的、亦即它采用的是全局感受野；同时由于各个神经元又是相对独立的、这直接导致它难以将原数据样本翻译成一个“视野”。而正如上面所说、CNN 采用的是局部感受野和共享权值，这在右图中的表现为它的神经元可以看成是“一整块”的“视野”，这块视野的每一个组成部分都是共享的权值（右图中的绿线；换句话说、右图中的四条绿线其实是同一个东西）在原数据样本的某一个局部上“看到”的东西

用上文中看风景的例子来说的话，CNN 的行为比较像一个正常人的表现、而 NN 的行为就更像是很多个能把整个风景都看在眼底的人同时看了同一个风景、然后分别感慨了一下并把这个感慨传递下去这种表现（？？？）

前向传导算法

CNN 的前向传导算法和上一章说明过的 NN 的前向传导算法有许多相似之处，至少从实现的层面来说它们的结构几乎一模一样。它们之间的不同之处则主要体现在如下两点：

接收的输入的形式不同
层与层之间的连接方式不同

先看第一点：对于 NN 而言、输入是一个 $N \times n$ 的矩阵

$X = \left( x_{1},\ldots,x_{N} \right)^{T}$

其中 $x_{1},\ldots,x_{N}$ 都是 $n \times 1$ 的列向量；当输入是图像时，NN 的处理方式是将图像拉直成一个列向量。以 $3 \times 3 \times 3$ 的图像为例（第一个 3 代指 RGB 通道，后两个 3 分别是高和宽），NN 会先把各个图像变成 $27 \times 1$ 的列向量（亦即 $n = 3 \times 3 \times 3$ ），然后再把它们合并、转置成一个 $N \times 27$ 的大矩阵以当作输入

CNN 则不会这么大费周章——它会直接以原始的数据作为输入。换句话说、CNN 接收的输入是 $N \times 3 \times 3 \times 3$ 的矩阵

可以用下图来直观认知一下该区别：

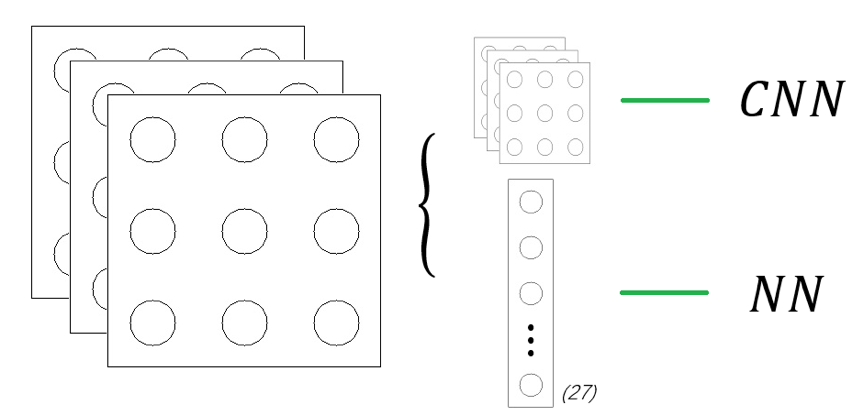
所以两者的前向传导算法就可以用以下两张图来进行直观说明了：

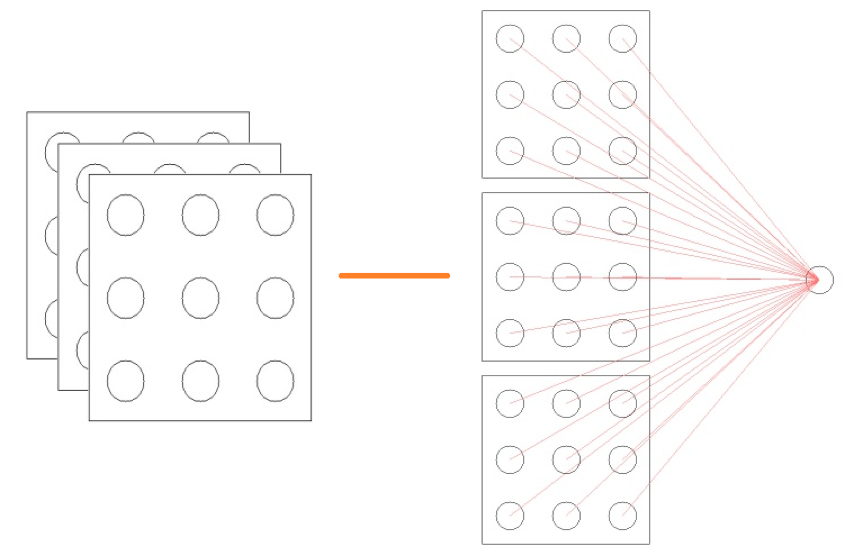
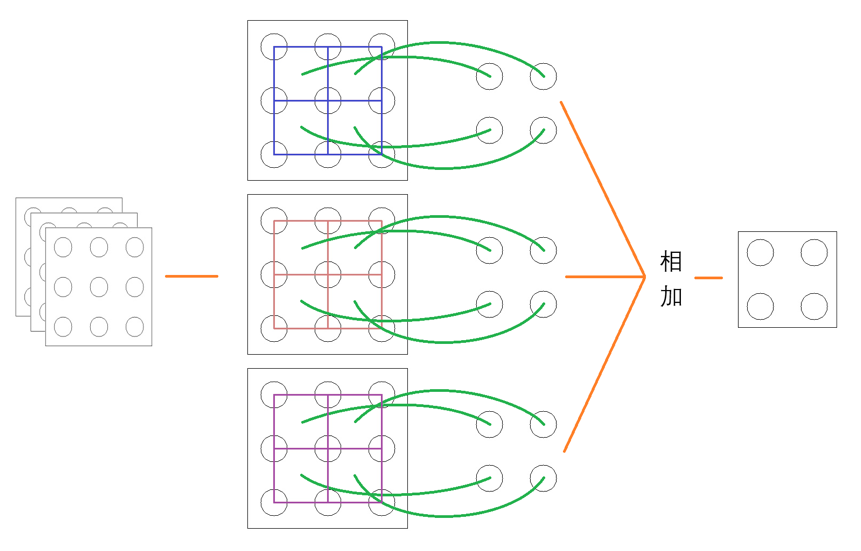
（我已经尽我全力来画得好看一点了……）

下面进行进一步的说明：

对于一个 $3 \times 3 \times 3$ 的输入，我们可以把它拆分成 3 个 $3 \times 3$ 的输入的堆叠（如果把 $3 \times 3 \times 3$ 的输入看成是一个“图像”的话，我们可以把拆分后的 3 个输入看成是该图像的 3 个“频道”；对于原始输入来讲，这 3 个频道通常就是 RGB 通道）
由于 NN 是全连接的，所以输入的所有信息都会直接输入给下一层的某个神经元
由于 CNN 是局部连接、共享权值的，一个合理的做法就是给拆分后的每个“频道”分配一个共享的“局部视野”（注意上图中三个“频道”中间都有 4 个相同颜色的正方形、且三个频道中正方形的颜色彼此不同，这就是局部共享视野的意义）（谁注意得到啊喂）。我们通常会把这三个局部视野视为一个整体并把它称作一个 Kernel 或一个 Filter
上面 CNN 那张图中我们用的是 $2 \times 2$ 的局部视野，该局部视野从相应频道左上看到右上、然后看左下、最后看右下，这个过程中一共看了四次、每看一次就会生成一个输出。所以三个局部视野会分别在对应的频道上生成四个输出、亦即一个 Kernel（或说一个 Filter）会生成 3 个 $2 \times 2$ 的输出，将它们直接相加就得到了该 Kernel 的最终输出——一个 $2 \times 2$ 的频道

上面最后提到的“左上 $\rightarrow$ 右上 $\rightarrow$ 左下 $\rightarrow$ 右下”这个“看”的过程其实就是所谓的“卷积”，这也正是卷积神经网络名字的由来。卷积本身的数学定义要比上面这个简单的描述要繁复得多，但幸运的是、实现和应用 CNN 本身并不需要具备这方面的数学理论知识（当然如果想开发更好的 CNN 结构与算法的话、是需要进行相关研究的，不过这些都已超出我们的讨论范围了）

注意：上面 CNN 的那张图中的情形为只有一个 Kernel 的情形，通常来说在实际应用中、我们会使用几十甚至几百个 Kernel 以期望网络能够学习出更好的特征——这是因为一个 Kernel 会生成一个频道，几十、几百个 Kernel 就意味着会生成几十、几百个频道，由此可以期待这大量不同的频道能够对数据进行足够强的描述（要知道原始数据可只有 3 个频道）

不难根据上文和上个系列的内容总结出 NN 和 CNN 目前为止的异同：

NN 和 CNN 的主要结构都是层，但是 NN 的层结构是一维的（ $1 \times n_{i}$ ）、CNN 的层结构是高维的
NN 处理的一般是“线性”的数据，CNN 则从直观上更适合处理“结构性的”数据
NN 层结构间会有权值矩阵作为连接的桥梁，CNN 则没有层结构之间的权值矩阵、取而代之的是层结构本身的局部视野。该局部视野会在前向传导算法中与层结构进行卷积运算来得到结果、并会直接将这个结果（或将被激活函数作用后的结果）传给下一层。因此我们常称 NN 中的层结构为“普通层”、称 CNN 中拥有局部视野的层结构为“卷积层”

可以看出、CNN 与 NN 区别之关键正在于“卷积”二字。虽然卷积的直观形式比较简单、但是它的实现却并不平凡。常用的解决方案有如下两种：

将卷积步骤变换成比较大规模的矩阵相乘（cs231n 里面的 stride trick 把我看哭了……）
利用快速傅里叶变换（Fast Fourier Transform，简称FFT）求解（只听说过，没实践过）

展开叙述它们需要用到比较深的知识、所以从略

最后介绍一下 Stride 和 Padding 的概念。Stride 可以翻译成“步长”，它描述了局部视野在频道上的“浏览速度”。设想现在有一个 $5 \times 5$ 的频道而我们的局部视野是 $2 \times 2$ 的，那么不同 Stride 下的表现将如下面两张图所示（只以第一排为例）：

（……）

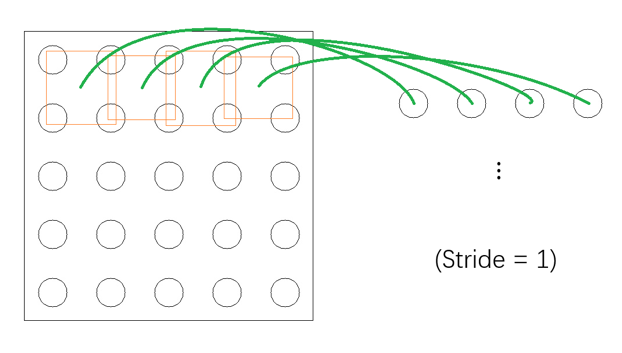
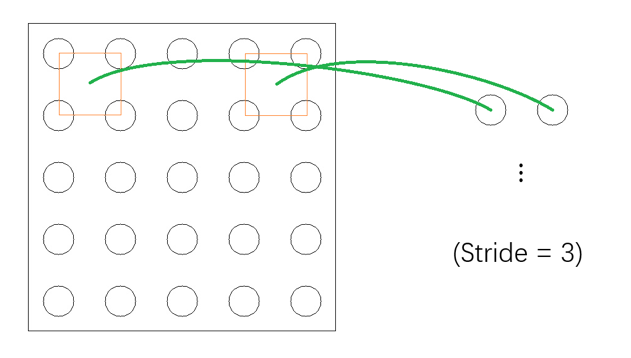
可以看到上图中局部视野每次前进“一步”而下图中每次会前进“三步”

Padding 可以翻译成“填充”、其存在意义有许多种解释，一种最好理解的就是——它能保持输入和输出的频道形状一致。注意目前为止展示过的栗子中，输入频道在被卷积之后、输出的频道都会“缩小”一点。这样在经过相当有限的卷积操作后、输入就会变得过小而不适合再进行卷积，从而就会大大限制了整个网络结构的深度。Padding 正是这个问题的一种解决方案：它会在输入频道进行卷积之前、先在频道的周围“填充”上若干圈的“0”。设想现在有一个 $3\times3$ 的频道而我们的局部视野也是 $3\times3$ 的，如果按照之前所说的卷积来做的话、不难想象输出将会是 $1\times1$ 的频道；不过如果我们将 Padding 设置为 1、亦即在输入的频道周围填充一圈 0 的话，那么卷积的表现将如下图所示：

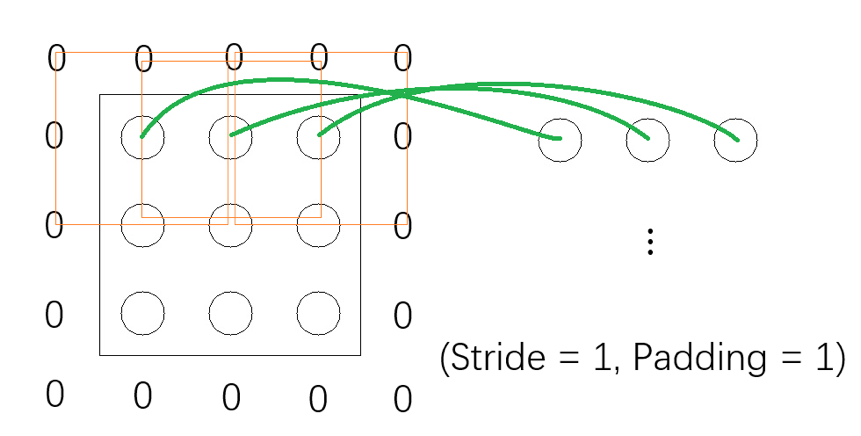
可以看到当我们在输入频道外面 Pad 上一圈 0 之后、输出就变成 $3 \times 3$ 的了，这为超深层 CNN 的搭建创造了可能性（比如有名的 ResNet）

在 cs231n 的这篇文章里面有一张很好很好很好的动图（大概位于页面中央），请允许我偷个懒不自己动手画了…… ( σ’ω’)σ

全连接层

全连接层是 Fully Connected Layer 的直译，常简称为 FC，它是可能会出现在 CNN 中的、一个比较特殊的结构；从名字就可以大概猜想到、FC 应该和普通层息息相关，事实上也正是如此。直观地说、FC 是连接卷积层和普通层的普通层，它将从父层（卷积层）那里得到的高维数据铺平以作为输入、进行一些非线性变换（用激活函数作用）、然后将结果输进跟在它后面的各个普通层构成的系统中：

上图中的 FC 一共有 $n_{1} = 3 \times 2 \times 2 = 12$ 个神经元，自 FC 之后的系统其实就是上一章所介绍的 NN。换句话说、我们可以把 CNN 拆分成如下两块结构：

自输入开始、至 FC 终止的“卷积块”，组成卷积块的都是卷积层
自 FC 开始、至输出终止的“NN 块”，组成 NN 块的都是普通层

注意：值得一提的是，在许多常见的网络结构中、NN 块里都只含有 FC 这个普通层

那么为什么 CNN 会有 FC 这个结构呢？或者问得更具体一点、为什么要将总体分成卷积块和NN块两部分呢？这其实从直观上来说非常好解释：卷积块中的卷积的基本单元是局部视野，用它类比我们的眼睛的话、就是将外界信息翻译成神经信号的工具，它能将接收的输入中的各个特征提取出来；至于 NN（神经网络）块、则可以类比我们的神经网络（甚至说、类比我们的大脑），它能够利用卷积块得到的信号（特征）来做出相应的决策。概括地说、CNN 视卷积块为“眼”而视 NN 块为“脑”，眼脑结合则决策自成（？？？）。用机器学习的术语来说、则卷积块为“特征提取器”而 NN 块为“决策分类器”

而事实上，CNN 的强大之处其实正在于其卷积块强大的特征提取能力上、NN 块甚至可以说只是用于分类的一个附属品而已。我们完全可以利用 CNN 将特征提取出来后、用前面几章介绍过的决策树、支持向量机等等来进行分类这一步而无须使用 NN 块

池化（Pooling）

池化是 NN 中完全没有的、只属于 CNN 的特殊演算。虽然名字听上去可能有些高大上的感觉，但它的本质其实就是“对局部信息的总结”。常见的池化有如下两种：

极大池化（Max Pooling），它会输出接收到的所有输入中的最大值
平均池化（Average Pooling），它会输出接收到的所有输入的均值

池化过程其实与卷积过程类似、可以看成是局部视野对输入信息的转换，只不过卷积过程做的是卷积运算、池化过程做的是极大或平均运算而已

不过池化与卷积有一点通常是差异较大的——池化的 Stride 通常会比卷积的 Stride 要大。比如对于一个 $3 \times 3$ 的输入频道和一个 $3 \times 3$ 的局部视野而言：

卷积常常选取 Stride 和 Padding 都为 1，从而输出频道是 $3 \times 3$ 的
池化常常选取 Stride 为 2、Padding 为1，从而输出频道是 $2 \times 2$ 的

将 Stride 选大是符合池化的内涵的：池化是对局部信息的总结、所以自然希望池化能够将得到的信息进行某种“压缩处理”。如果将 Stride 选得比较小的话、总结出来的信息就很可能会产生“冗余”，这就违背了池化的本意

不过为什么最常见的两种池化——极大池化和平均池化确实能够压缩信息呢？这主要是因为 CNN 一般处理的都是图像数据。由经验可知、图像在像素级间隔上的差异是很小的，这就为上述两种池化提供了一定的合理性