MergedNB 的实现

（本文会用到的所有代码都在这里）

本文主要介绍混合型朴素贝叶斯—— MergedNB 的实现。（我知道的）混合型朴素贝叶斯算法主要有两种提法：

• 用某种分布的密度函数算出训练集中各个样本连续型特征相应维度的密度之后，根据这些密度的情况将该维度离散化、最后再训练离散型朴素贝叶斯模型
• 直接结合离散型朴素贝叶斯和连续型朴素贝叶斯： $$y = f(x^{*}) = \arg{\max_{c_k}{p\left( y = c_{k} \right)\prod_{j \in S_{1}}^{}{p(X^{\left( j \right)} = {x^{*}}^{\left( j \right)}|y = c_{k})}\prod_{j \in S_{2}}^{}{p(X^{j} = {x^{*}}^{\left( j \right)}|y = c_{k})}}}$$

从直观可以看出、第二种提法可能会比第一种提法要“激进”一些，因为如果某个连续型维度采用的分布特别“大起大落”的话、该维度可能就会直接“主导”整个决策。但是考虑到实现的简洁和直观（……），我们还是演示第二种提法的实现。感兴趣的观众老爷可以尝试实现第一种提法，思路和过程都是没有太本质的区别的、只是会繁琐不少

我们可以对气球数据集 1.0 稍作变动、将“气球大小”这个特征改成“气球直径”，然后我们再手动做一次分类以加深对混合型朴素贝叶斯算法的理解。新数据集如下表所示（不妨称之为气球数据集 2.0）：

颜色	直径	测试人员	测试动作	结果
黄色	10	成人	用手打	不爆炸
黄色	15	成人	用脚踩	爆炸
黄色	9	小孩	用手打	不爆炸
黄色	9	小孩	用脚踩	不爆炸
黄色	19	成人	用手打	爆炸
黄色	21	成人	用脚踩	爆炸
黄色	16	小孩	用手打	不爆炸
黄色	22	小孩	用脚踩	爆炸
紫色	10	成人	用手打	不爆炸
紫色	12	小孩	用手打	不爆炸
紫色	22	成人	用脚踩	爆炸
紫色	21	小孩	用脚踩	爆炸

该数据集的电子版本可以参见这里。我们想预测的是样本：

颜色	大小	测试人员	测试动作
紫色	10	小孩	用脚踩

除了“大小”变成了“直径”、其余特征都一点未变，所以我们只需再计算直径的条件概率（密度）即可。由 GaussianNB 的算法可知：

$${\hat{\mu}}_{不爆炸} = \frac{10 + 9 + 9 + 16 + 10 + 12}{6} = 11$$ $${\hat{\mu}}_{爆炸} = \frac{15 + 19 + 21 + 22 + 22 + 21}{6} = 20$$ $${\hat{\sigma}}_{不爆炸} = \frac{1}{6}\left\lbrack \left( 10 - {\hat{\mu}}_{不爆炸} \right)^{2} + \ldots + \left( 12 - {\hat{\mu}}_{不爆炸} \right)^{2} \right\rbrack = 6$$ $${\hat{\sigma}}_{爆炸} = \frac{1}{6}\left\lbrack \left( 15 - {\hat{\mu}}_{爆炸} \right)^{2} + \ldots + \left( 21 - {\hat{\mu}}_{爆炸} \right)^{2} \right\rbrack = 6$$

从而

$$\hat{p}\left( 不爆炸\right) = \frac{1}{\sqrt{2\pi}{\hat{\sigma}}_{不爆炸}}e^{- \frac{\left( 10 - {\hat{\mu}}_{不爆炸} \right)^{2}}{2{\hat{\sigma}}^{2}_{不爆炸}}} \times p\left( 小孩\middle| 不爆炸\right) \times p\left( 用脚踩\middle| 不爆炸\right) \approx 0.0073$$ $$\hat{p}\left( 爆炸\right) = \frac{1}{\sqrt{2\pi}{\hat{\sigma}}_{爆炸}}e^{- \frac{\left( 10 - {\hat{\mu}}_{爆炸} \right)^{2}}{2{\hat{\sigma}}^{2}_{爆炸}}} \times p\left( 小孩\middle| 爆炸\right) \times p\left( 用脚踩\middle| 爆炸\right) \approx 0.0046$$

因此我们应该认为给定样本所导致的结果是“不爆炸”，这和直观大体相符。接下来看看具体应该如何进行实现，首先是初始化：

from b_NaiveBayes.Original.Basic import *
from b_NaiveBayes.Original.MultinomialNB import MultinomialNB
from b_NaiveBayes.Original.GaussianNB import GaussianNB

class MergedNB(NaiveBayes):
    """
        初始化结构
        self._whether_discrete：记录各个维度的变量是否是离散型变量
        self._whether_continuous：记录各个维度的变量是否是连续型变量
        self._multinomial、self._gaussian：离散型、连续型朴素贝叶斯模型
    """
    def __init__(self, whether_continuous):
        self._multinomial, self._gaussian = (
            MultinomialNB(), GaussianNB()
        if whether_continuous is None:
            self._whether_discrete = self._whether_continuous = None
        else:
            self._whether_continuous = np.array(whether_continuous)
            self._whether_discrete = ~self._whether_continuous

然后是和模型的训练相关的实现，这一块将会大量重用之前在 MultinomialNB 和 GaussianNB 里面写过的东西：

def feed_data(self, x, y, sample_weight=None):
    if sample_weight is not None:
        sample_weight = np.array(sample_weight)
    x, y, wc, features, feat_dics, label_dic = DataUtil.quantize_data(
        x, y, wc=self._whether_continuous, separate=True)
    # 若没有指定哪些维度连续，则用 quantize_data 中朴素的方法判定哪些维度连续
    if self._whether_continuous is None:
        self._whether_continuous = wc
        # 通过Numpy中对逻辑非的支持进行快速运算
        self._whether_discrete = ~self._whether_continuous
    # 计算通用变量
    self.label_dic = label_dic
    discrete_x, continuous_x = x
    cat_counter = np.bincount(y)
    self._cat_counter = cat_counter
    labels = [y == value for value in range(len(cat_counter))]
    # 训练离散型朴素贝叶斯
    labelled_x = [discrete_x[ci].T for ci in labels]
    self._multinomial._x, self._multinomial._y = x, y
    self._multinomial._labelled_x, self._multinomial._label_zip = (
        labelled_x, list(zip(labels, labelled_x)))
    self._multinomial._cat_counter = cat_counter
    self._multinomial._feat_dics = [_dic
        for i, _dic in enumerate(feat_dics) if self._whether_discrete[i]]
    self._multinomial._n_possibilities = [len(feats)
        for i, feats in enumerate(features) if self._whether_discrete[i]]
    self._multinomial.label_dic = label_dic
    # 训练连续型朴素贝叶斯
    labelled_x = [continuous_x[label].T for label in labels]
    self._gaussian._x, self._gaussian._y = continuous_x.T, y
    self._gaussian._labelled_x, self._gaussian._label_zip = labelled_x, labels
    self._gaussian._cat_counter, self._gaussian.label_dic = cat_counter, label_dic
    # 处理样本权重
    self._feed_sample_weight(sample_weight)

# 分别利用 MultinomialNB 和 GaussianNB 处理样本权重的方法来处理样本权重
def feed_sample_weight(self, sample_weight=None):
    self._multinomial.feed_sample_weight(sample_weight)
    self._gaussian.feed_sample_weight(sample_weight)

# 分别利用 MultinomialNB 和 GaussianNB 的训练函数来进行训练
def _fit(self, lb):
    self._multinomial.fit()
    self._gaussian.fit()
    p_category = self._multinomial.get_prior_probability(lb)
    discrete_func, continuous_func = (
        self._multinomial["func"], self._gaussian["func"])
    # 将 MultinomialNB 和 GaussianNB 的决策函数直接合成最终决策函数
    # 由于这两个决策函数都乘了先验概率、我们需要除掉一个先验概率
    def func(input_x, tar_category):
        input_x = np.array(input_x)
        return discrete_func(
            input_x[self._whether_discrete].astype(
                np.int), tar_category) * continuous_func(
            input_x[self._whether_continuous], tar_category) / p_category[tar_category]
    return func

（又臭又长啊喂)

上述实现有一个显而易见的可以优化的地方：我们一共在代码中重复计算了三次先验概率、但其实只用计算一次就可以。考虑到这一点不是性能瓶颈，为了代码的连贯性和可读性、我们就没有进行这个优化（？？？）

数据转换函数则相对而言要复杂一点，因为我们需要跳过连续维度、将离散维度挑出来进行数值化：

# 实现转换混合型数据的方法，要注意利用 MultinomialNB 的相应变量
def _transfer_x(self, x):
    _feat_dics = self._multinomial["feat_dics"]
    idx = 0
    for d, discrete in enumerate(self._whether_discrete):
        # 如果是连续维度，直接调用 float 方法将其转为浮点数
        if not discrete:
            x[d] = float(x[d])
        # 如果是离散维度，利用转换字典进行数值化
        else:
            x[d] = _feat_dics[idx][x[d]]
        if discrete:
            idx += 1
    return x

至此，混合型朴素贝叶斯模型就搭建完毕了。为了比较合理地对它进行评估，我们不妨采用 UCI 上一个我认为有些病态的数据集进行测试。问题的描述大概可以概括如下：

“训练数据包含了某银行一项业务的目标客户的信息、电话销售记录以及后来他是否购买了这项业务的信息。我们希望做到：根据客户的基本信息和历史联系记录，预测他是否会购买这项业务”。UCI 上的原问题描述则如下图所示：

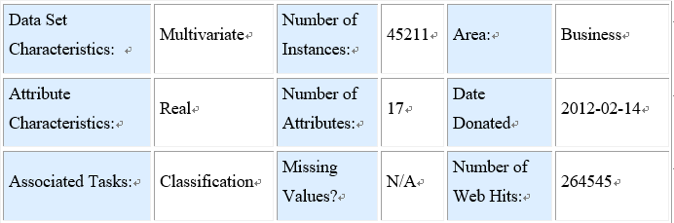
概括其主要内容、就是它是一个有 17 个属性的二类分类问题。之所以我认为它是病态的，是因为我发现即使是 17 个属性几乎完全一样的两个人，他们选择是否购买业务的结果也会截然相反。事实上从心理学的角度来说，想要很好地预测人的行为确实是一项非常困难的事情、尤其是当该行为直接牵扯到较大的利益时

完整的数据集可以参见这里（最后一列数据是类别）。按照数据的特性、我们可以通过和之前用来评估 MultinomialNB 的代码差不多的代码（注意额外定义一个记录离散型维度的数组即可）得出如下图所示的结果：

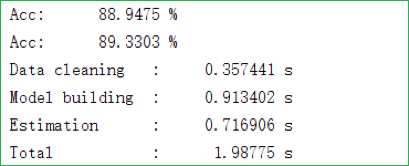
虽然准确率达到了 89%左右，但其实该问题不应该用准确率作为评判的标准。因为如果我们观察数据就会发现、数据存在着严重的非均衡现象。事实上，88%的客户最终都是没有购买这个业务的、但我们更关心的是那一小部分购买了业务的客户，这种情况我们通常会用 F1-score 来衡量模型的好坏。此外，该问题非常需要人为进行数据清洗、因为其原始数据非常杂乱。此外，我们可以对该问题中的各个离散维度进行可视化。该数据共 9 个离散维度，我们可以将它们合并在同一个图中以方便获得该数据离散部分的直观（如下图所示；由于各个特征的各个取值通常比较长（比如”manager”之类的），为整洁、我们直接将横坐标置为等差数列而没有进行转换）：

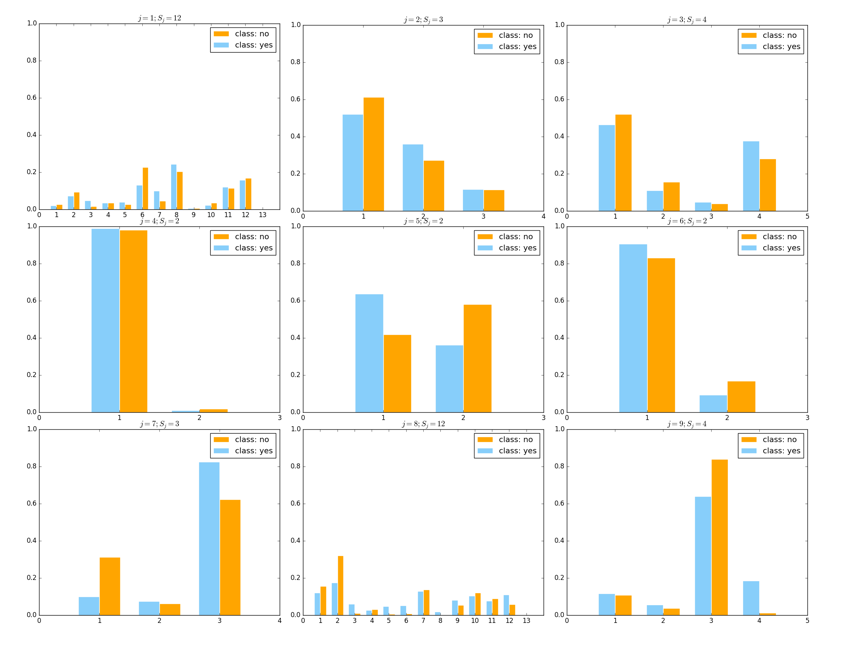
其中天蓝色代表类别 yes、亦即购买了业务；橙色则代表 no、亦即没有购买业务。可以看到、所有离散维度的特征都是前面所说的“无足轻重”的特征

连续维度的可视化是几乎同理的，唯一的差别在于它不是柱状图而是正态分布密度函数的函数曲线。具体的代码实现从略、感兴趣的观众老爷们可以尝试动手实现一下，这里仅放出程序运行的结果。该数据共 7 个连续维度，我们同样把它们放在同一个图中：

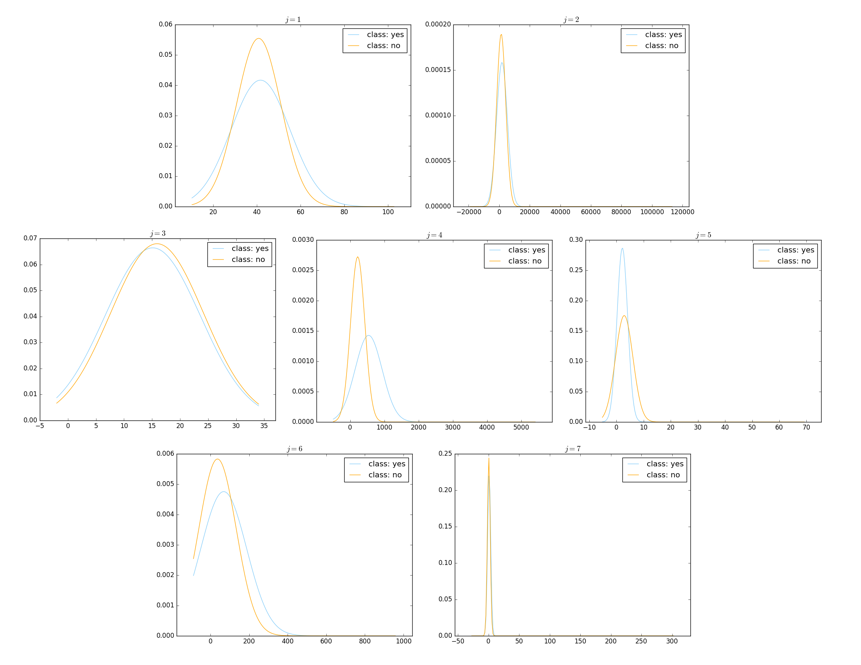
其中，天蓝色曲线代表类别 yes、橙色曲线代表类别 no。可以看到，两种类别的数据在各个维度上的正态分布的均值、方差都几乎一致

从以上的分析已经可以比较直观地感受到、该问题确实相当病态。特别地，考虑到朴素贝叶斯的算法、不难想象此时的混合型朴素贝叶斯模型基本就只是根据各类别的先验概率来进行分类决策

至此，朴素贝叶斯算法的理论、实现就差不多都说了一遍。作为收尾，下篇文章会补上之前没有展开叙述的一些细节、同时也会简要地介绍一下其余的贝叶斯分类器