核模型的实现与评估

发表于 | 分类于

有了上一篇文章的诸多准备、我们就能以之为基础实现核感知机和 SVM 了。不过需要指出的是，由于我们实现的 SVM 是一个朴素的版本、所以如果是要在实际任务中应用 SVM 的话，还是应该使用由前人开发、维护并经过长年考验的成熟的库（比如 LibSVM 等）；这些库能够处理更大的数据和更多的边值情况、运行的速度也会快上很多，这是因为它们通常都使用了底层语言来实现核心算法、且在算法上也做了许多数值稳定性和数值优化的处理

核感知机的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
import numpy as np
from Util.Bases import KernelBase
class KernelPerceptron(KernelBase):
    def __init__(self):
        KernelBase.__init__(self)
        # 对于核感知机而言、循环体中所需的额外参数是学习速率（默认为1）
        self._fit_args, self._fit_args_names = [1], ["lr"]
    # 更新dw
    def _update_dw_cache(self, idx, lr, sample_weight):
        self._dw_cache = lr * self._y[idx] * sample_weight[idx]
    # 更新db
    def _update_db_cache(self, idx, lr, sample_weight):
        self._db_cache = self._dw_cache
    # 利用和训练样本中的类别向量y来更新w和b
    def _update_params(self):
        self._w = self._alpha * self._y
        self._b = np.sum(self._w)
    def _fit(self, sample_weight, lr):
        # 获取加权误差向量
        _err = (np.sign(self._prediction_cache) != self._y) * sample_weight
        # 引入随机性以进行随机梯度下降
        _indices = np.random.permutation(len(self._y))
        # 获取“错得最严重”的样本所对应的下标
        _idx = _indices[np.argmax(_err[_indices])]
        # 若该样本被正确分类、则所有样本都已正确分类，此时返回真值、退出训练循环体
        if self._prediction_cache[_idx] == self._y[_idx]:
            return True
        # 否则、进行随机梯度下降
        self._alpha[_idx] += lr
        self._update_dw_cache(_idx, lr, sample_weight)
        self._update_db_cache(_idx, lr, sample_weight)
        self._update_pred_cache(_idx)

可以看到代码清晰简洁，这主要得益于核感知机算法本身比较直白。我们可以先通过螺旋线数据集来大致看看它的分类能力、结果如下图所示：

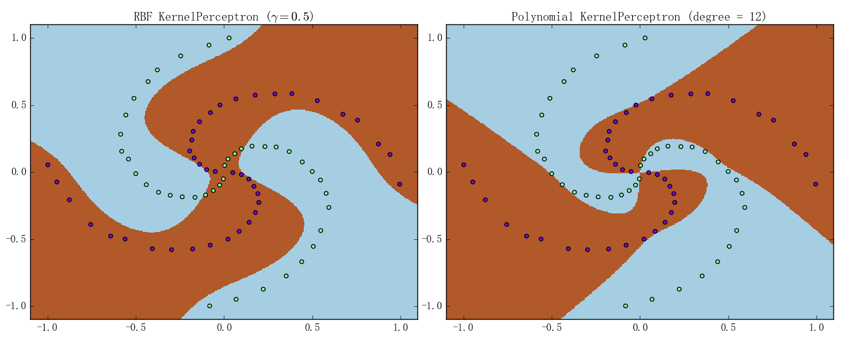
p1.png

左图为 RBF 核感知机（）、准确率为 90.0%；右图为多项式核感知机（）、准确率为 98.75%（迭代次数都是）。虽说效果貌似还不错，但是由它们的训练曲线可以看出、训练过程其实是相当“不稳定”的：

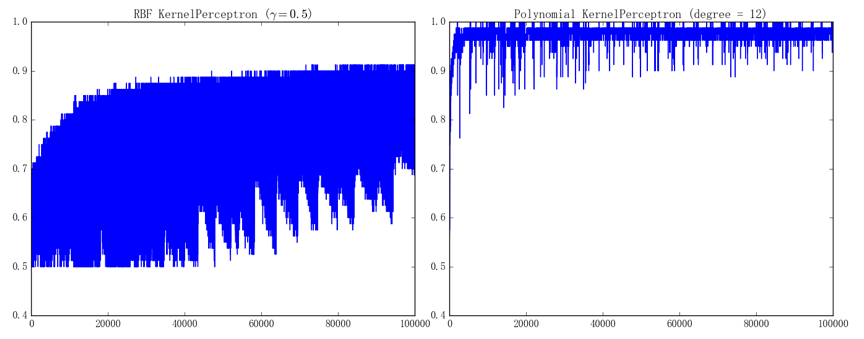
p2.png

左、右图分别对应着 RBF 核感知机和多项式核感知机的训练曲线。之所以有这么大的波动、是因为我们采取的随机梯度下降每次只会进行非常局部的更新，而螺旋线数据集本身又具有比较特殊的结构，从而在直观上也能想象、模型的参数在训练的过程中很容易来回震荡。这一点在 SVM 上也会有体现、因为我们打算实现的 SMO 算法同样也是针对局部（两个变量）进行更新的

核 SVM 的实现

接下来就看看核 SVM 的实现，虽说有些繁复、但其实只是一步一步地将之前说过的算法翻译出来而已，如果能理顺算法的逻辑的话、实现本身其实并不困难：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
import numpy as np
from Util.Bases import KernelBase, KernelConfig
class SVM(KernelBase, metaclass=SubClassChangeNamesMeta):
    def __init__(self):
        KernelBase.__init__(self)
        # 对于核SVM而言、循环体中所需的额外参数是容许误差（默认为）
        self._fit_args, self._fit_args_names = [1e-3], ["tol"]
        self._c = None
    # 实现SMO算法中、挑选出第一个变量的方法
    def _pick_first(self, tol):
        con1 = self._alpha > 0
        con2 = self._alpha < self._c
        # 算出损失向量并拷贝成3份
        err1 = self._y * self._prediction_cache - 1
        err2 = err1.copy()
        err3 = err1.copy()
        # 将相应的数位置为0
        err1[con1 | (err1 >= 0)] = 0
        err2[(~con1 | ~con2) | (err2 == 0)] = 0
        err3[con2 | (err3 <= 0)] = 0
        # 算出总的损失向量并取出最大的一项
        err = err1 ** 2 + err2 ** 2 + err3 ** 2
        idx = np.argmax(err)
        # 若该项的损失小于则返回返回空值
        if err[idx] < tol:
            return
        # 否则、返回对应的下标
        return idx
    # 实现SMO算法中、挑选出第二个变量的方法（事实上是随机挑选）
    def _pick_second(self, idx1):
        idx = np.random.randint(len(self._y))
        while idx == idx1:
            idx = np.random.randint(len(self._y))
        return idx
    # 获取新的的下界
    def _get_lower_bound(self, idx1, idx2):
        if self._y[idx1] != self._y[idx2]:
            return max(0., self._alpha[idx2] - self._alpha[idx1])
        return max(0., self._alpha[idx2] + self._alpha[idx1] - self._c)
    # 获取新的的上界
    def _get_upper_bound(self, idx1, idx2):
        if self._y[idx1] != self._y[idx2]:
            return min(self._c, self._c + self._alpha[idx2] - self._alpha[idx1])
        return min(self._c, self._alpha[idx2] + self._alpha[idx1])
    # 更新dw
    def _update_dw_cache(self, idx1, idx2, da1, da2, y1, y2):
        self._dw_cache = np.array([da1 * y1, da2 * y2])
    # 更新db
    def _update_db_cache(self, idx1, idx2, da1, da2, y1, y2, e1, e2):
        gram_12 = self._gram[idx1][idx2]
        b1 = -e1 - y1 * self._gram[idx1][idx1] * da1 - y2 * gram_12 * da2
        b2 = -e2 - y1 * gram_12 * da1 - y2 * self._gram[idx2][idx2] * da2
        self._db_cache = (b1 + b2) * 0.5
    # 利用和训练样本中的类别向量y来更新w和b
    def _update_params(self):
        self._w = self._alpha * self._y
        _idx = np.argmax((self._alpha != 0) & (self._alpha != self._c))
        self._b = self._y[_idx] – np.sum(self._alpha * self._y * self._gram[_idx])

以上就是 SMO 算法中的核心步骤，接下来只需要将它们整合进一个大框架中即可（需要指出的是，随机选取第二个变量虽说效果也不错、但效率终究还是会差上一点；不过考虑到实现的复杂度、我们还是用随机选取的方法来进行实现）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
# 定义局部更新参数的方法
def _update_alpha(self, idx1, idx2):
    l, h = self._get_lower_bound(idx1, idx2), self._get_upper_bound(idx1, idx2)
    y1, y2 = self._y[idx1], self._y[idx2]
    e1 = self._prediction_cache[idx1] - self._y[idx1]
    e2 = self._prediction_cache[idx2] - self._y[idx2]
    eta = self._gram[idx1][idx1] + self._gram[idx2][idx2] - 2 * self._gram[idx1][idx2]
    a2_new = self._alpha[idx2] + (y2 * (e1 - e2)) / eta
    if a2_new > h:
        a2_new = h
    elif a2_new < l:
        a2_new = l
    a1_old, a2_old = self._alpha[idx1], self._alpha[idx2]
    da2 = a2_new - a2_old
    da1 = -y1 * y2 * da2
    self._alpha[idx1] += da1
    self._alpha[idx2] = a2_new
    # 根据、来更新dw和db并局部更新
    self._update_dw_cache(idx1, idx2, da1, da2, y1, y2)
    self._update_db_cache(idx1, idx2, da1, da2, y1, y2, e1, e2)
    self._update_pred_cache(idx1, idx2)
# 初始化惩罚因子C
def _prepare(self, **kwargs):
    self._c = kwargs.get("c", KernelConfig.default_c)
def _fit(self, sample_weight, tol):
    idx1 = self._pick_first(tol)
    # 若没能选出第一个变量、则所有样本的误差都，此时返回真值、退出训练循环体
    if idx1 is None:
        return True
    idx2 = self._pick_second(idx1)
    self._update_alpha(idx1, idx2)

可以看到大部分代码确实只是算法的直译。同样可以先通过螺旋线数据集来大致看看核 SVM 的分类能力、结果如下图所示（图中用黑圈标注的样本点即是支持向量）：

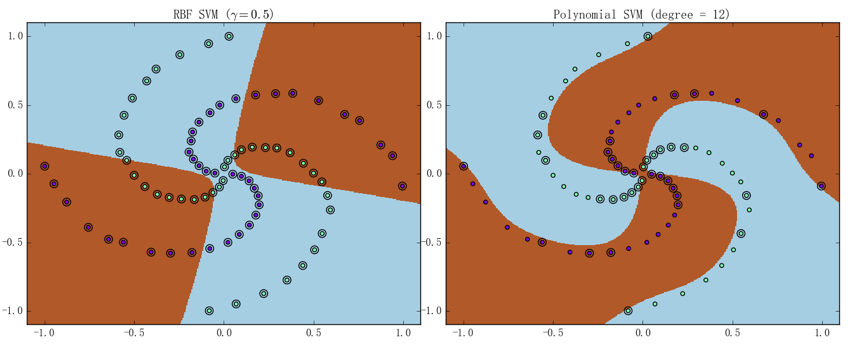
p3.png

左图为 RBF 核 SVM（）、迭代了 729 次即达到了停机条件（所有样本的误差都）、最终准确率为 51.25%；右图为多项式核 SVM（）、迭代了 6727 次即达到了停机条件、准确率为 97.5%。它们的训练曲线如下图所示：

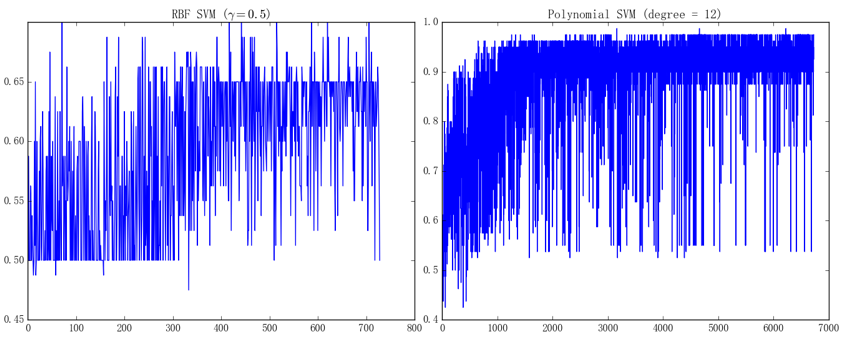
p4.png

左、右图分别对应着 RBF 核 SVM 和多项式核 SVM 的训练曲线。虽说看上去似乎比核感知机的表现还要差、但这毕竟只是一个特殊的情形；事实上、即使是成熟的 SVM 库也并不是万能的。比如如果直接使用螺旋线数据集来训练 sklearn 中的、基于 LibSVM 进行实现的 SVM 模型的话、会得到如下图所示的结果：

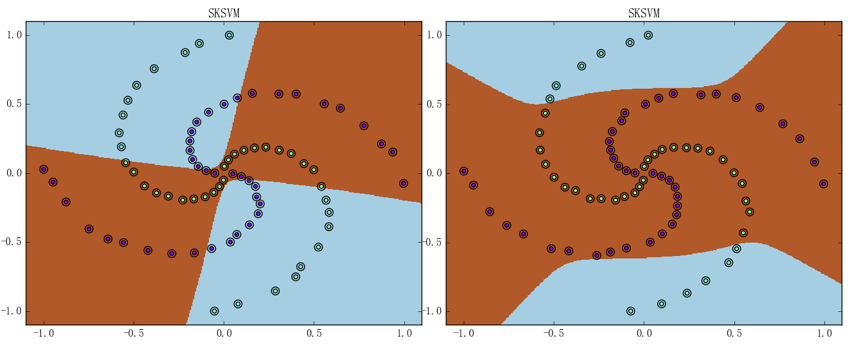
p5.png

左图为 RBF 核 SVM（）、最终准确率为 50.0%；右图为多项式核 SVM（）、准确率为 65.0%。造成这种差异的原因在于我们实现的多项式核函数和 sklearn 中的 SVM 所使用的多项式核函数不一样，如果将我们的核函数传进去、是可以得到相似结果的

作为本篇文章的收尾，我们可以通过画出两种核模型在蘑菇数据集上的训练曲线来简单地评估一下模型在真实数据下的表现。为了说明模型的泛化能力，我们只取 100 个样本作为训练样本、并用剩余 8000 多个样本作为测试样本来检验

首先来看一下核感知机的表现：

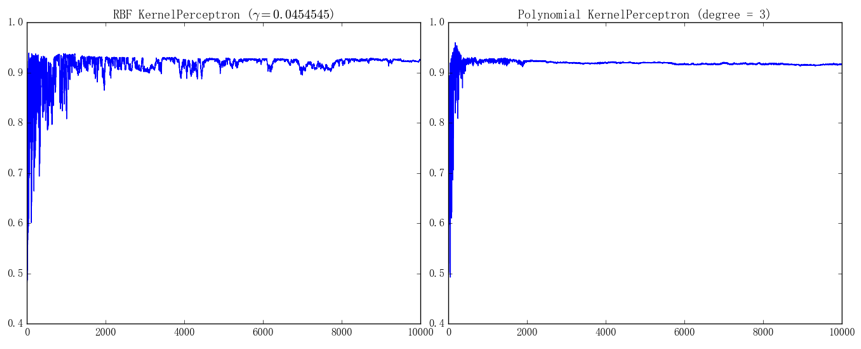
p6.png

左图为 RBF 核感知机（）的训练曲线、最终在测试集上的准确率为 92.53%；右图为多项式核感知机（）的训练曲线、最终在测试集上的准确率为 91.59%（迭代次数都是）。由于只采用了 100 个样本训练、每次训练后的模型表现会波动得比较厉害；不过总体而言、RBF 核感知机会比多项式核感知机波动得更厉害一点

接下来看一下核 SVM 的表现：

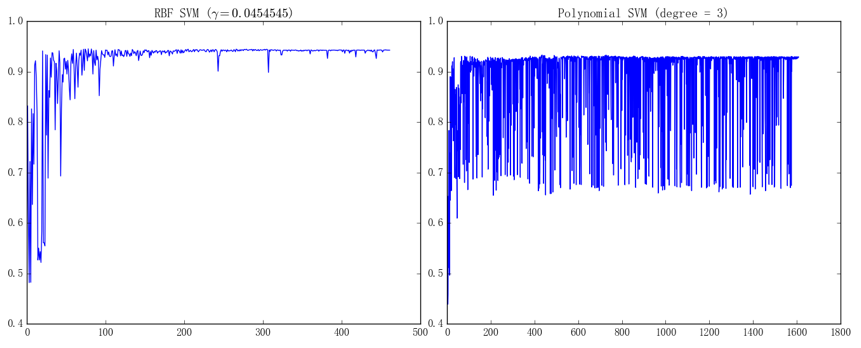
p7.png

左图为 RBF 核 SVM（）、迭代了 462 次即达到了停机条件、最终在测试集上的准确率为 94.29%；右图为多项式核 SVM（）、迭代 1609 次即达到了停机条件、最终在测试集上的准确率为 92.96%

观众老爷们能赏个脸么 ( σ'ω')σ