从线性到非线性

发表于 | 分类于

前文已经提过，由于对偶形式中的样本点仅以内积的形式出现、所以利用核技巧能将线性算法“升级”为非线性算法。有一个与核技巧（Kernel Trick）类似的概念叫核方法（Kernel Method），这两者的区别可以简单地从字面意思去认知：当我们提及核方法（Method）时、我们比较注重它背后的原理；当我们提及核技巧（Trick）时、我们更注重它实际的应用。考虑到本书的主旨、我们还是选择了核技巧这一说法

注意：以上关于核技巧和核方法这两个名词的区分不是一种共识、而是我个人为了简化问题而作的一种形象的说明，所以切忌将其作为严谨的叙述

核技巧简述

虽说重视应用、但一些基本的概念还是需要稍微了解的。核方法本身要深究的话会牵扯到诸如正定核、内积空间、希尔伯特空间乃至于再生核希尔伯特空间（Reproducing Kernel Hilbert Space，常简称为 RKHS）、这些东西又会牵扯到泛函的相关理论，可谓是一个可以单独拿来出书的知识点。幸运的是，单就核技巧而言、我们仅需要知道其中的三个定理即可，这三个定理分别说明了核技巧的合理性、普适性和高效性。不过在叙述这三个定理之前，我们可以先来看看核技巧的直观解释

核技巧往简单地说，就是将一个低维的线性不可分的数据映射到一个高维的空间、并期望映射后的数据在高维空间里是线性可分的。我们以异或数据集为例：在二维空间中、异或数据集是线性不可分的；但是通过将其映射到三维空间、我们可以非常简单地让其在三维空间中变得线性可分。比如定义映射：

该映射的效果如下图所示：

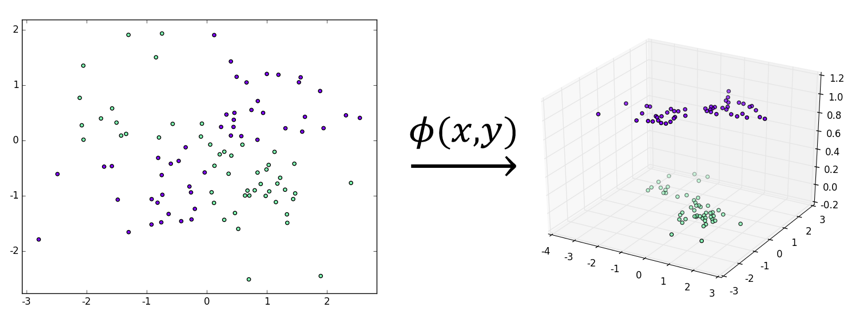
p1.png

可以看到，虽然左图的数据集线性不可分、但显然右图的数据集是线性可分的，这就是核技巧工作原理的一个不太严谨但仍然合理的解释

注意：这里我们暂时采用了“从低维到高维的映射”这一说法、但该说法并不完全严谨，原因会在后文说明、这里只需留一个心眼即可

从直观上来说，确实容易想象、同一份数据在越高维的空间中越有可能线性可分，但从理论上是否确实如此呢？1965 年提出的 Cover 定理解决了这个问题，它的具体叙述如下：若设 d 维空间中 N 个点线性可分的概率为，那么就有：

其中

定理的证明细节从略，我们只需要知道它证明了当空间的维数 d 越大时、其中的 N 个点线性可分的概率就越大，这构成了核技巧的理论基础之一

至此，似乎问题就转化为了如何寻找合适的映射、使得数据集在被它映射到高维空间后变得线性可分。不过可以想象的是，现实任务中的数据集要比上文我们拿来举例的异或数据集要复杂得多、直接构造一个恰当的的难度甚至可能高于解决问题本身。而核技巧的巧妙之处就在于，它能将构造映射这个过程再次进行转化、从而使得问题变得简易：它通过核函数来避免显式定义映射。往简单里说、核技巧会通过用核函数

替换各式算法中出现的内积

来完成将数据从低维映射到高维的过程。换句话说、核技巧的思想如下：

  • 将算法表述成样本点内积的组合（这经常能通过算法的对偶形式实现）
  • 设法找到核函数，它能返回样本点、被作用后的内积
  • 用替换、完成低维到高维的映射（同时也完成了从线性算法到非线性算法的转换）

而核技巧事实上能够应用的场景更为宽泛——在 2002 年由 Schlkopf 和 Smola 证明的表示定理告诉我们：设为核函数对应的映射后的空间（RKHS），表示中的范数，那么对于任意单调递增的函数和任意非负损失函数、优化问题

的解总可以表述为核函数的线性组合

这意味着对于任意一个损失函数和一个单调递增的正则化项组成的优化问题、我们都能够对其应用核技巧。所以至此、大多数的问题就转化为如何找到能够表示成高维空间中内积的核函数了。幸运的是、1909 年提出的 Mercer 定理解决了这个问题，它的具体叙述如下：若满足

亦即如果是对称函数的话、那么它具有 Hilbert 空间中内积形式的充要条件有以下两个：

  • 对任何平方可积、满足
  • 对含任意 N 个样本的数据集、核矩阵： 是半正定矩阵

注意：通常我们会称满足这两个充要条件之一的函数为 Mercer 核函数而把核函数定义得更宽泛。由于本书不打算在理论上深入太多、所以一律将 Mercer 核函数简称为核函数。此外，虽说 Mercer 核函数确实具有 Hilbert 空间中的内积形式、但此时的 Hilbert 空间并不一定具有“维度”这么好的概念（或说、可以认为此时 Hilbert 空间的维度为无穷大，比如下面马上就要讲到的 RBF 核、它映射后的空间就是无穷维的）。这也正是为何前文说“从低维到高维的映射”不完全严谨

Mercer 定理为寻找核函数带来了极大的便利。可以证明如下两族函数都是核函数：

  • 多项式核
  • 径向基（Radial Basis Function，常简称为RBF）核

核技巧的应用

我们接下来会实现的也正是这两族核函数对应的、应用了核技巧的算法，具体而言、我们会利用核技巧来将感知机和支持向量机算法从原始的线性版本“升级”为非线性版本

由简入繁、先从核感知机讲起；由于感知机对偶算法十分简单、对其应用核技巧相应的也非常平凡——直接用核函数替换掉相应内积即可。不过需要注意的是，由于我们采用的是随机梯度下降、所以算法中也应尽量只更新局部参数以避免进行无用的计算：

  1. 输入：训练数据集、迭代次数 M、学习速率，其中：

  2. 过程：

    1. 初始化参数：

      同时计算核矩阵：

    2. 对：

      1. 若（亦即没有误分类的样本点）则退出循环体
      2. 否则，任取中的一个样本点并利用其下标更新局部参数：
      3. 利用和更新预测向量： 其中、表示的第 i 行、表示全为 1 的向量
  3. 输出：感知机模型

再来看如何对 SVM 应用核技巧。虽说在对偶算法上应用核技巧是非常自然、直观的，但是直接在原始算法上应用核技巧也无不可

注意原始问题可以表述为：

若令、其中：

则可知上述问题能够通过映射到高维空间上：

亦即

利用一定的技巧是可以直接利用梯度下降法直接对这个无约束最优化问题求解的，不过相关的数学理论基础都相当繁复、实现起来也有些麻烦；尽管如此、还是有许多优秀的算法是基于上述思想的

直观起见、我们还是将重点放在如何对 SMO 应用核技巧的讨论上。由于前文已经说明了 SMO 的大致步骤，所以我们先补充说明当时没有讲到的、选出两个变量后应该如何继续求解，然后再来看具体的算法应该如何叙述

使得对、都有

不妨设、，那么在针对、的情况下，是固定的、且上述最优化问题可以转化为：

使得对和、有

其中为常数。可以看出此时问题确实转化为了一个带约束的二次函数求极值问题、从而能够比较简单地求出其解析解。推导过程从略、以下就直接在算法中写出结果：

  1. 输入：训练数据集、迭代次数 M、容许误差，其中：

  2. 过程：

    1. 初始化参数： 同时计算核矩阵：

    2. 对：

      1. 选出违反 KKT 条件最严重的样本点，若其违反程度小于、则退出循环体

      2. 否则、选出异于i的任一个下标 j，针对和构造一个新的只有两个变量二次规划问题并求出解析解。具体而言，首先要更新的是、它由以下几个参数定出：

        考虑到约束条件、我们需要定出新的下上界：

        继而根据和对进行“裁剪”即可：

        这里要注意记录的增量：

      3. 利用更新、同时注意记录的增量：
      4. 利用、进行局部更新： 其中
      5. 利用和更新预测向量： 其中、`$\mathbf{K}_{\mathbf{i}\mathbf{\cdot}}$表示$\mathbf{K}$的第i行、$\mathbf{1}$表示全为1的向量
  3. 输出：感知机模型、其中：

这里的下标 k 满足

可以用反证法证明这样的下标 k 必存在、具体步骤从略

从这两种算法应用核技巧的方式可以看出，虽然它们应用的训练算法完全不同（一个是随机梯度下降、一个是序列最小最优化）、但它们每一次迭代中做的事情却有相当多是一致的；为了合理重复利用代码、我们可以先把对应的实现都抽象出来：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
class KernelBase(ClassifierBase):
    """
        初始化结构
        self._fit_args, self._args_names：记录循环体中所需额外参数的信息的属性
        self._x, self._y, self._gram：记录数据集和Gram矩阵的属性
            self._w, self._b, self._alpha：记录各种参数的属性
        self._kernel, self._kernel_name, self._kernel_param：记录核函数相关信息的属性
            self._prediction_cache, self._dw_cache, self._db_cache：记录 、dw、db的属性
    """
    def __init__(self):
        super(KernelBase, self).__init__()
        self._fit_args, self._fit_args_names = None, []
        self._x = self._y = self._gram = None
        self._w = self._b = self._alpha = None
        self._kernel = self._kernel_name = self._kernel_param = None
        self._prediction_cache = self._dw_cache = self._db_cache = None
    # 定义计算多项式核矩阵的函数
    @staticmethod
    def _poly(x, y, p):
        return (x.dot(y.T) + 1) ** p
    # 定义计算RBF核矩阵的函数
    @staticmethod
    def _rbf(x, y, gamma):
        return np.exp(-gamma * np.sum((x[..., None, :] - y) ** 2, axis=2))

其中定义 RBF 核函数时用到了升维的操作、这算是 Numpy 的高级使用技巧之一；具体的思想和机制会在后续的文章中进行简要说明、这里就暂时按下不表

以上我们就搭好了基本的框架、接下来要做的就是继续把具有普适性的训练过程进行抽象和实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
# 默认使用RBF核、默认迭代次数epoch为一万次
def fit(self, x, y, kernel="rbf", epoch=10 ** 4, **kwargs):
    self._x, self._y = np.atleast_2d(x), np.array(y)
    if kernel == "poly":
        # 对于多项式核、默认使用KernelConfig中的default_p作为p的取值
        _p = kwargs.get("p", KernelConfig.default_p)
        self._kernel_name = "Polynomial"
        self._kernel_param = "degree = {}".format(_p)
        self._kernel = lambda _x, _y: KernelBase._poly(_x, _y, _p)
    elif kernel == "rbf":
         # 对于RBF核、默认使用样本x的维数n的倒数1/n作为的取值
        _gamma = kwargs.get("gamma", 1 / self._x.shape[1])
        self._kernel_name = "RBF"
        self._kernel_param = "gamma = {}".format(_gamma)
        self._kernel = lambda _x, _y: KernelBase._rbf(_x, _y, _gamma)
    # 初始化参数
    self._alpha, self._w, self._prediction_cache = (
        np.zeros(len(x)), np.zeros(len(x)), np.zeros(len(x)))
    self._gram = self._kernel(self._x, self._x)
    self._b = 0
    # 调用 _prepare方法进行特殊参数的初始化（比如SVM中的惩罚因子C）
    self._prepare(**kwargs)
    # 获取在循环体中会用到的参数
    _fit_args = []
    for _name, _arg in zip(self._fit_args_names, self._fit_args):
        if _name in kwargs:
            _arg = kwargs[_name]
        _fit_args.append(_arg)
    # 迭代、直至达到迭代次数epoch或 _fit核心方法返回真值
    for _ in range(epoch):
        if self._fit(sample_weight, *_fit_args):
            break
    # 利用和训练样本来更新w和b
    self._update_params()

注意到我们调用了一个叫KernelConfig的类、它的定义很简单：

1
2
3
class KernelConfig:
    default_c = 1
    default_p = 3

亦即默认惩罚因子为 1、多项式核的次数为 3。同时需要注意的是，我们在循环体里面调用了_fit核心方法、在最后调用了_update_params方法，这两个方法都是留给子类定义的；不过比较巧妙的是，无论是记录的_prediction_cache的更新还是预测函数predict的定义、都可以写成同一种形式：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 定义更新预测向量 _prediction_cache的函数
def _update_pred_cache(self, *args):
    self._prediction_cache += self._db_cache
    if len(args) == 1:
        self._prediction_cache += self._dw_cache * self._gram[args[0]]
    else:
        self._prediction_cache += self._dw_cache.dot(self._gram[args, ...])
# 定义预测函数
def predict(self, x, get_raw_results=False):
    # 计算测试集和训练集之间的核矩阵并利用它来做决策
    x = self._kernel(np.atleast_2d(x), self._x)
    y_pred = x.dot(self._w) + self._b
    if not get_raw_results:
        return np.sign(y_pred)
    return y_pred
观众老爷们能赏个脸么 ( σ'ω')σ