特殊的层结构

发表于 | 分类于

在神经网络模型中有一类特殊的 Layer 结构——它们不会独立地存在、而会“依附”在某个 Layer 之后以实现某种特定的功能。一般我们会称这种特殊的 Layer 结构为附加层（SubLayer）

CostLayer 算是一个比较特殊的 SubLayer：它附加在输出层的后面、能够根据输出进行相应的变换并得到模型的损失。“根据输出得到损失”即是 CostLayer 实现的特定的功能。对于一般的 SubLayer、它的思想是清晰的：为了在 Layer 的输出的基础上进行一些变换以得到更好的输出；换句话说、SubLayer 通常可以优化 Layer 的输出

对于 SubLayer 和 SubLayer、SubLayer 和 Layer 之间的关系，我们可以类比于决策树中的根节点（Root）、叶节点（Leaf）等概念来提出“根层（Root Layer）”和“叶层（Leaf Layer）”的概念。不妨以下图为例：

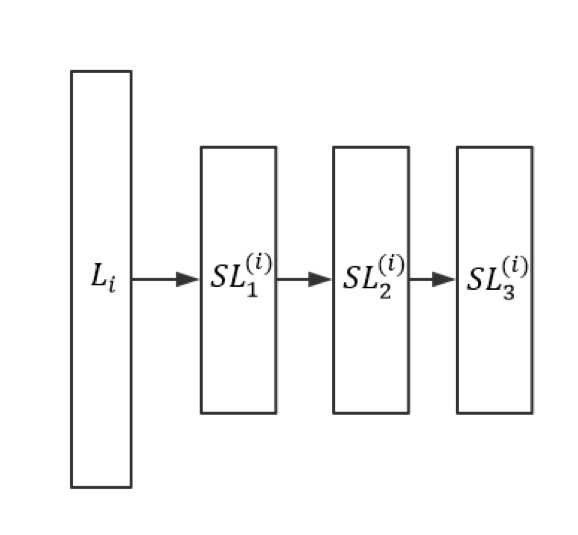
p1.png

其中为第 i 层 Layer、为附加在后的三个 SubLayer，且：

  • 分别为的父层
  • 分别为的子层
  • 为的 Root Layer
  • 为的 Leaf Layer

从 SubLayer 的思想可以看出、SubLayer 很像一个“局部优化器”；不过和下一节中要介绍的优化器不同，它不是通过更新模型参数来优化模型、而是通过变换 Layer 的输出来优化模型

在进一步叙述之前、我们需要先定义一下层结构之间的“关联”是什么。具体而言：

  • Layer 和 Layer 之间的关联即为相应的权值矩阵，比如之间的关联即为
  • SubLayer 之间的关联亦即 SubLayer 和 Root Layer 之间的关联都只是“占位符”、它们没有任何实际的作用。这其实是符合 SubLayer 作为“局部优化器”的定位的

从而 SubLayer 的所有行为大体上可以概括如下：

  • 在前向传导中、它会根据自身的属性和算法来优化从父层处得到的更新
  • 在反向传播中、它会有如下三种行为：
    • SubLayer 之间的关联以及 SubLayer 和 Root Layer 之间的关联不会被更新、因为它们仅仅是占位符
    • SubLayer 作为“局部优化器”、本身可能会有一些参数，这些参数则可能会被 BP 算法更新、但影响域仅在该 SubLayer 的内部（Normalize 会是一个很好的例子）
    • Layer 之间的关联的更新是通过 Leaf Layer 完成的。具体而言、的 Leaf Layer 会利用的激活函数来完成局部梯度的计算

最后这里所谓的“利用 Leaf Layer”可以通过下面两张图来直观认知在存在 SubLayer 的情况下、前向传导算法和反向传播算法的表现：

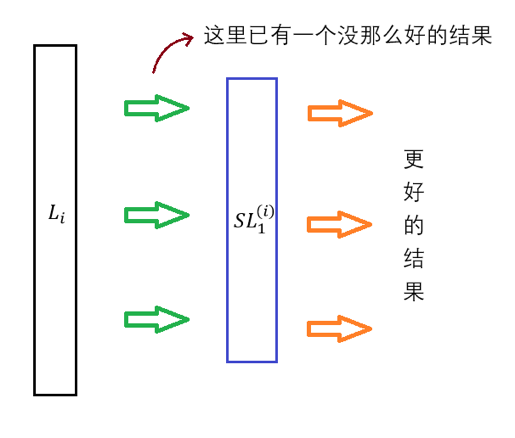
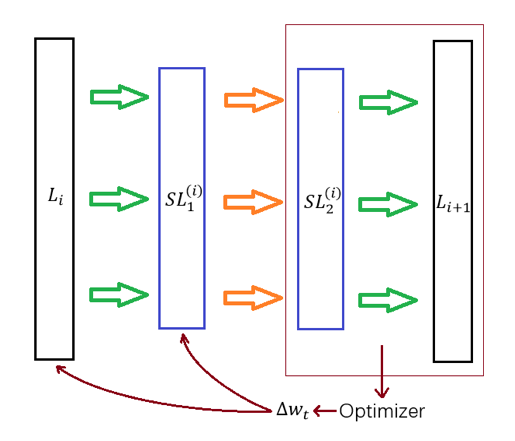
p2.png p3.png

典型的 SubLayer 有前文提到过的 Dropout 和 Normalize。它们都是近年来才提出的技术，其中 Dropout 是由 Srivastava 等人在 Journal of Machine Learning Research 15 (2014） 上的一篇论文中最先提出的、全文共 30 页，感兴趣的读者可以直接参见这里；Normalize 则是 Batch Normalization 对应的特殊层结构、它是由 Sergey loffe 和 Christian Szegedy 在 2015 年最先提出的，感兴趣的读者可以直接参见这里，这里仅直观地进行一些说明：

  • Dropout 的核心思想在于提高模型的泛化能力：它会在每次迭代中依概率去掉对应 Layer 的某些神经元，从而每次迭代中训练的都是一个小的神经网络
  • Normalize 的核心思想在于把父层的输出进行“归一化”、从而期望能够解决由于网络结构过深而引起的“梯度消失”等问题

虽说实现 SubLayer 本身并不是一个特别困难的任务，但是处理 SubLayer 之间的关联、SubLayer 与 Layer 之间的关联以及反向传播算法却是一件相当麻烦的事；具体的实现细节比较繁杂、这里就不进行叙述了。观众老爷们可以尝试按照上文相关的思想和定义来进行实现、我个人实现的版本则可以参见这里

注意：我们会在下个系列的文章中利用 Tensorflow 框架进行相关的实现，彼时我们会结合具体实现对 Dropout 和 Normalize 进行深入一些的介绍

至此、神经网络会用到的所有层结构就都大致说明了一遍，接下来就要解决一个至关重要但又还没解决的问题了：如何使用局部梯度来更新相应 Layer 中的参数

观众老爷们能赏个脸么 ( σ'ω')σ