感知机确实能够解决线性可分数据集的分类问题，但从它的解法容易看出、感知机的解是有无穷多个的。这主要是因为它对自己的要求太低：只需对训练集中所有样本点都能正确分类即可。换句话说、感知机基本没有考虑模型的泛化能力，这就导致感知机有时会训练出如下图所示的结果：

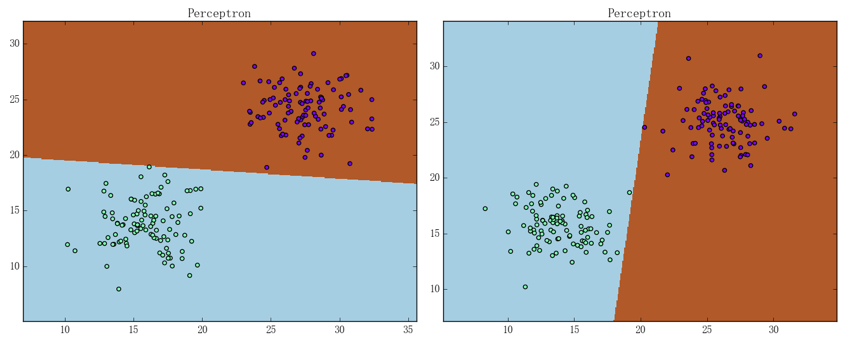
可以看出它们是不尽合理的。支持向量机（SVM）针对这一点提出了一种改进方法，本篇文章主要叙述的就是该改进的思想和具体内容

间隔最大化与线性 SVM

上图的结果之所以显得不合理、主要是因为分离超平面离正负样本点集都显得“太近”了。因此一个自然的想法就是：在训练过程中考虑上超平面到点集的距离、并努力让这个距离最大化

然而直接从集合出发定义集合到平面的距离是相对困难的、所以通常会将它转化为点到平面的距离。前文已经说过，对于样本点 $(x_{i},y_{i})$ 而言、它到超平面 $\Pi:w \cdot x + b = 0$ 的相对距离即为：

$d^{*}\left( x_{i},\Pi \right) = |w \cdot x_{i} + b|$

这里的相对距离 $d^{*}$ 有一个更学术一点称谓——函数间隔（Functional Margin）。函数间隔有一个比较明显的缺陷就是、当 $w$ 和 $b$ 等比例变大或变小时，虽然超平面不会改变、但是 $d^{*}$ 却会随之等比例变大或变小。为解决这个问题、我们可以比较自然地定义出所谓的几何间隔（Geometric Distance）：

$d\left( x_{i},\Pi \right) = \frac{1}{\left\| w \right\|} \cdot d^{*}\left( x_{i},\Pi \right) = \frac{1}{\left\| w \right\|} \cdot |w \cdot x_{i} + b|$

这里的 $\left\| w \right\|$ 是 $w$ 的欧式范数。顾名思义、几何间隔描述的就是向量 $x_{i}$ 到超平面 $\Pi$ 的几何距离（欧氏距离），它不会随 $w$ 和 $b$ 的等比例变化而变化、是相对稳定且直观意义优良的距离的定义方法。SVM 在训练过程中所引入的也正是各个样本点到当前分离超平面的几何距离，结合前文所说的“努力让超平面到点集的距离最大化”、SVM 算法就可以比较自然地叙述为：最大化（几何间隔） $d$ 、使得：

$\frac{1}{\left\| w \right\|} \cdot \left\lbrack y_{i}\left( w \cdot x_{i} + b \right) \right\rbrack \geq d\ (i = 1,\ldots,N)$

考虑到几何间隔和函数间隔之间的转换关系、该问题可以等价为：最大化 $\frac{d^{*}}{\left\| w \right\|}$ 、使得：

$y_{i}\left( w \cdot x_{i} + b \right) \geq d^{*}\ (i = 1,\ldots,N)$

可以发现函数间隔 $d^{*}$ 的取值其实对该优化问题的解没有影响。这是因为当 $d^{*}$ 变成 $\lambda d^{*}$ 时、 $w$ 和 $b$ 也会相应地变成 $\lambda w$ 和 $\lambda b$ （在超平面不变的情况下），此时 $\frac{d^{*}}{\left\| w \right\|}$ 和不等式约束都没有变、所以对优化问题确实没有影响。这样的话我们就能不妨设 $d^{*} = 1$ 、从而优化问题就可以转换为：最大化 $\frac{1}{\left\| w \right\|}$ 、使得：

$y_{i}\left( w \cdot x_{i} + b \right) \geq 1\ (i = 1,\ldots,N)$

易知该优化问题又能转化为：最小化 $\frac{1}{2}\left\| w \right\|^{2}$ 、使得：

$y_{i}\left( w \cdot x_{i} + b \right) - 1 \geq 0\ (i = 1,\ldots,N)$

这就是 SVM 算法的最原始的形式。可以证明，只要训练集 $D$ 线性可分、那么 SVM 算法对应的这个优化问题的解就存在且唯一；其中存在性的证明相对直观、唯一性的证明需要用到反证法和一些数学上的技巧，细节从略

假设该优化问题的解为 $w^{*}$ 和 $b^{*}$ ，我们通常称超平面：

$\Pi^{*}:w^{*} \cdot x + b^{*} = 0$

为 $D$ 的最大硬间隔分离超平面。之所以称它为“硬间隔”的理由会在后文叙述，这里暂时按下不表。需要指出的是，考虑到优化问题中的不等式约束、易知在超平面

$\Pi_{1}^{*}:w^{*} \cdot x + b = - 1$

和超平面

$\Pi_{2}^{*}:w^{*} \cdot x + b = + 1$

之间、是没有任何 $D$ 中的样本点的。不过在 $\Pi_{1}^{*}$ 和 $\Pi_{2}^{*}$ 上、确实有可能有样本点。我们通常称 $\Pi_{1}^{*}$ 和 $\Pi_{2}^{*}$ 为间隔边界、称其上的某些点为支持向量

注意：也有间隔边界上的样本点全是支持向量的说法，本书采用的支持向量的定义将更“苛刻”一些，具体细节会在 SVM 算法的对偶形式的叙述中讲到

以上的叙述比较完整地说明了 SVM 如何应用于线性可分的数据集，接下来我们就看看如何将这种思想拓展到线性不可分数据集的分类之上。事实上，由于单用超平面的话、甚至连对线性不可分数据集正确分类都做不到，更不用提在此之上的将（硬）间隔最大化的问题了；但是考虑到间隔最大化的思想、我们可以做一定的“妥协”：将“硬”间隔转化为更加普适的“软”间隔。从数学的角度来说，这等价于将不等式约束放宽：

$y_{i}\left( w \cdot x_{i} + b \right) \geq 1 \rightarrow y_{i}\left( w \cdot x_{i} + b \right) \geq 1 - \xi_{i}$

其中的 $\xi_{i}$ 通常被称为“松弛变量”，它需要满足 $\xi_{i} \geq 0$ 。当然、这个约束的放宽并不是没有代价的，我们要在需要最小化的 ${\frac{1}{2}\left\| w \right\|}^{2}$ 上加进一个“惩罚项”来“惩罚” $\xi_{i}$ 。换句话说，我们需要最小化的项将变为：

$L\left( w,b,x,y \right) = \frac{1}{2}\left\| w \right\|^{2} + C\sum_{i = 1}^{N}\xi_{i}$

式中 $L(w,b,x,y)$ 即为损失函数、损失函数中的 $C$ （ $> 0$ ）通常被称为“惩罚因子”，它描述了对松弛变量 $\xi_{i}$ 的“惩罚力度”： $C$ 越大意味着最终的 SVM 模型越不能容忍误分类的点，越小则反之

综上所述、SVM 算法对应的优化问题可以拓展为：最小化 $L(w,b,x,y)$ 、使得：

$y_{i}\left( w \cdot x_{i} + b \right) \geq 1 - \xi_{i}\ (i = 1,\ldots,N)$

其中

$\xi_{i} \geq 0\ (i = 1,\ldots,N)$

可以证明该优化问题的解存在、且 $w$ 的解唯一但 $b$ 的解不唯一，证明细节从略。同时参照感知机算法、自然希望能够写出使用随机梯度下降来训练软间隔最大化 SVM 的算法；但是注意到 $L$ 表达式中的 $\xi_{i}$ 是有约束的（需要不小于 0）、所以直接对其进行随机梯度下降存在一定的困难。为了将问题近似转化为无约束最优化问题、我们可以引入 Hinge 损失，其定义很简单：

$l\left( w,b,x,y \right) = \max(0,1 - y\left( w \cdot x + b \right))$

其中 $y \in \left\{ - 1, + 1 \right\}$ 。换句话说，只有在模型作出足够肯定的正确的预测时、Hinge 损失才为 0；否则即使模型作出了正确的预测、Hinge 损失还是有可能给予模型一个惩罚

利用 Hinge 损失、我们可以把损失函数 $L$ 写成：

$\hat{L}\left( w,b,x,y \right) = \frac{1}{2}\left\| w \right\|^{2} + C\sum_{i = 1}^{N}{l(w,b,x_{i},y_{i})}$

并通过最小化 $\hat{L}$ 来求解上述 SVM 算法对应的最优化问题

注意：最小化 $\hat{L}$ 和上文最优化问题的等价性可能并不太显然，但是通过对比损失函数及逐条比对约束条件、完成等价性证明不算太困难（比如直接令 $\xi_{i} = l(w,b,x_{i},y_{i})$ ）

由于我们想要写出随机梯度下降的算法、所以求出 $\hat{L}$ 在单一样本 $(x_{i},y_{i})$ 上对 $w$ 和 $b$ 的偏导数是有必要的：

$\begin{align} \frac{\partial\hat{L}(w,b,x_{i},y_{i})}{\partial w} &= w + \left\{ \begin{matrix} 0,\ \ & y_{i}\left( w \cdot x_{i} + b \right) \geq 1 \\ - Cy_{i}x_{i},\ \ & y_{i}\left( w \cdot x_{i} + b \right) < 1 \\ \end{matrix} \right.\ \\ \frac{\partial\hat{L}(w,b,x_{i},y_{i})}{\partial b} &= \left\{ \begin{matrix} 0,\ \ & y_{i}\left( w \cdot x_{i} + b \right) \geq 1 \\ - Cy_{i},\ \ & y_{i}\left( w \cdot x_{i} + b \right) < 1 \\ \end{matrix} \right.\ \end{align}$

有了这两个偏导数之后，模仿感知机算法、我们就可以比较轻松地写出软间隔最大化 SVM 的随机梯度下降训练算法：

输入：训练数据集 $D = \{\left( x_{1},y_{1} \right),\ldots,\left( x_{N},y_{N} \right)\}$ 、迭代次数 M、惩罚因子 $C$ 、学习速率 $\eta$ ，其中： $x_{i} \in X \subseteq \mathbb{R}^{n}\ ;y_{i} \in Y = \{ - 1,\ + 1\}$
过程：
1. 初始化参数： $w = \left( 0,\ldots,0 \right)^{T} \in \mathbb{R}^{n},b = 0$
2. 对：
  1. 算出误差向量 $e = \left( e_{1},\ldots,e_{N} \right)^{T}$ 、其中： $e_{i} = 1 - y_{i}(w \cdot x_{i} + b)$
  2. 取出误差最大的一项： $i = \arg{\min_{i}e_{i}}$
  3. 若 $e_{i} \leq 0$ 则直接退出循环体、否则取对应的样本来进行随机梯度下降 $\begin{align} w &\leftarrow (1 - \eta)w + \eta Cy_{i}x_{i} \\ b &\leftarrow b + \eta Cy_{i} \end{align}$
输出：线性 SVM 模型 $g\left( x \right) = \text{sign}\left( f\left( x \right) \right) = sign\left( w \cdot x + b \right)$

需要指出的是，虽然算法看上去差不多、内核也都是随机梯度下降，但其实在感知机模型对学习速率不敏感的同时、线性 SVM 对学习速率是相当敏感的。由前文提到过的 Novikoff 定理和凸优化相关理论可以从理论上解释这个现象，囿于篇幅、这里就不展开叙述了

由于上述线性 SVM 算法的实现和感知机算法的实现几乎一致、所以我们就略去对线性 SVM 实现的详细说明；观众老爷们可以参照感知机的代码来尝试进行实现、我个人实现的版本则可以参见这里

可以通过二维线性可分数据集来简单直观地感受一下感知机和线性 SVM 的区别、结果如下图所示：

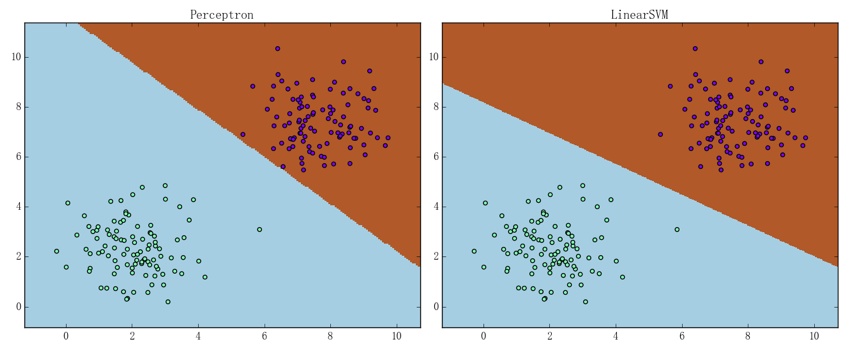
其中左、右图分别为感知机和线性 SVM 的表现，可以看出线性 SVM 要更合理

SVM 算法的对偶形式

与感知机类似、SVM 算法也是存在着对偶形式，不过这个转化的过程会比感知机那里的转化过程复杂不少。具体的推导步骤会放在相关数学理论中、这里我们就直接看结果：

硬间隔最大化的对偶形式 $\max_{\alpha}{- \frac{1}{2}\sum_{i = 1}^{N}{\sum_{j = 1}^{N}{\alpha_{i}\alpha_{j}y_{i}y_{j}\left( x_{i} \cdot x_{j} \right)}} + \sum_{i = 1}^{N}\alpha_{i}}$ 使得对 $i = 1,\ldots,N$ 、都有： $\sum_{i = 1}^{N}{\alpha_{i}y_{i}} = 0$ $\alpha_{i} \geq 0$
软间隔最大化的对偶形式 $\max_{\alpha}{- \frac{1}{2}\sum_{i = 1}^{N}{\sum_{j = 1}^{N}{\alpha_{i}\alpha_{j}y_{i}y_{j}\left( x_{i} \cdot x_{j} \right)}} + \sum_{i = 1}^{N}\alpha_{i}}$ 使得对 $i = 1,\ldots,N$ 、都有： $\sum_{i = 1}^{N}{\alpha_{i}y_{i}} = 0$ $0 \leq \alpha_{i} \leq C$

可以看到它们彼此之间相似度非常高、且转化的过程和感知机的转化过程也多少有些相似。同样的，由于对偶形式中样本点仅以内积的形式出现、我们通常会先把 Gram 矩阵算出来。现我们假设对偶形式的解为 $\alpha^{*} = \left( \alpha_{1},\ldots,\alpha_{N} \right)^{T}$ 、那么就有：

$\begin{align} w^{*} &= \sum_{i = 1}^{N}{\alpha_{i}^{*}y_{i} \cdot x_{i}} \\ b^{*} &= y_{j} - \sum_{i = 1}^{N}{y_{i}\alpha_{i}^{*}\left( x_{i} \cdot x_{j} \right)} \end{align}$

其中 $w^{*}$ 的表达式和感知机中 $w^{*}$ 的表达式一致、 $b^{*}$ 表达式中出现的 j 是满足 $0 < \alpha_{j} < C$ 的下标（用反证法可以证明这种 j 必然存在，细节从略）

在有了对偶形式之后、我们就可以叙述支持向量的一个比较“苛刻”的定义了：假设支持向量的集合为 $SV$ 、那么

在硬间隔最大化 SVM 中： $x_{i} \in SV \Leftrightarrow \alpha_{i}^{*} > 0$
在软间隔最大化 SVM 中： $x_{i} \in SV \Leftrightarrow 0 < \alpha_{i}^{*} \leq C$

其中在软间隔最大化 SVM 里，由于 $\alpha_{i}^{*} \leq C$ 本身其实是由约束条件规定的、所以可以把上述两式统一写成：

$x_{i} \in SV \Leftrightarrow \alpha_{i}^{*} > 0$

我们可以通过下图来直观认知何谓支持向量：

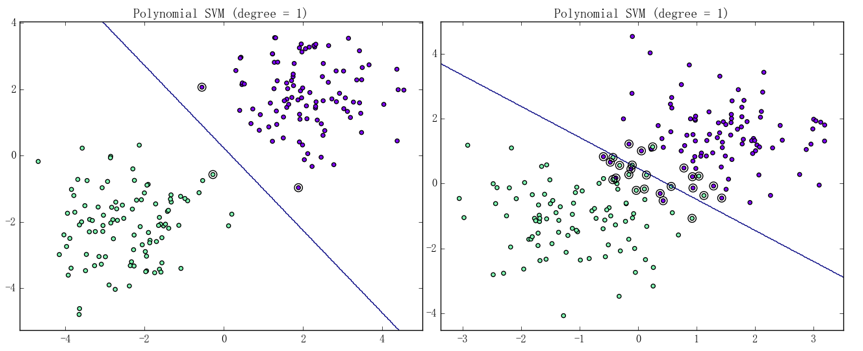
图中的线段即为决策边界、被一个黑色圆圈给圈住的样本点即为支持向量，左图为线性可分数据集上的情况、右图为线性不可分数据集上的情况

此外，说明 $\alpha_{i}^{*}$ 和 $\xi_{i}^{*}$ 是如何定出各个样本点和间隔边界、分离超平面之间的位置关系是有必要的，它能加深我们对对偶形式求解过程中涉及到的 KKT 条件的理解与记忆（KKT 条件的相关定义会在相关数学理论中讲到）。具体而言：

若 $\alpha_{i}^{*} = 0$ ，那么 $x_{i}$ 被正确分类且不在间隔边界上、又或被正确分类且在间隔边界上但不是支持向量
若 $0 < \alpha_{i}^{*} < C$ ，那么就有 $\xi_{i} = 0$ 、亦即 $x_{i}$ 落在间隔边界上且为支持向量
若，那么：
- 若 $\xi_{i} = 0$ 、则 $x_{i}$ 落在间隔边界上且为支持向量
- 若 $0 < \xi_{i} < 1$ 、则 $x_{i}$ 被正确分类且落在间隔边界和分离超平面之间
- 若 $\xi_{i} = 1$ 、则 $x_{i}$ 落在分离超平面上
- 若 $\xi_{i} > 1$ 、则 $x_{i}$ 被错误分类
  由此可知、 $\xi_{i}$ 其实刻画了 $x_{i}$ 到相应间隔边界的函数间隔。换句话说、 $\frac{\xi_{i}}{\left\| w \right\|}$ 即是 $x_{i}$ 到间隔边间的距离（几何间隔）

SVM 的训练

前文曾经提过、原始算法的对偶形式通常能将问题简化；虽然这点在感知机算法上没有太多体现，但是对于 SVM 来说，由于它的应用场景更为广泛、在许多问题的提法下转化成对偶形式的意义将非常重大。目前已经有许多针对 SVM 的成熟算法，本书拟介绍的是其中由 Platt 在 1998 年提出的、针对对偶问题求解的序列最小最优化算法（SMO）。本篇文章主要介绍 SMO 的思路和大概步骤，详细的叙述会在下一篇文章介绍完核技巧后进行

SMO 是一种启发式算法，其主要手段是在每次迭代中专注于只有两个变量的优问题以期望在可以接受的时间内得到一个较优解。具体而言、SMO 要解决的是软间隔最大化 SVM 的对偶问题：

$\max_{\alpha}{- \frac{1}{2}\sum_{i = 1}^{N}{\sum_{j = 1}^{N}{\alpha_{i}\alpha_{j}y_{i}y_{j}\left( x_{i} \cdot x_{j} \right)}} + \sum_{i = 1}^{N}\alpha_{i}}$

使得对 $i = 1,\ldots,N$ 、都有：

$\sum_{i = 1}^{N}{\alpha_{i}y_{i}} = 0$ $0 \leq \alpha_{i} \leq C$

解决方案是在循环体中不断针对两个变量构造二次规划、并通过求出其解析解来优化原始的对偶问题。大致步骤如下：

考察所有变量（ $\alpha_{1},\ldots,\alpha_{N}$ ）及对应的样本点（ $\left( x_{1},y_{1} \right),\ldots,(x_{N},y_{N})$ ）满足 KKT 条件的情况
若所有变量及对应样本在容许误差内都满足 KKT 条件，则退出循环体、完成训练
否则、通过如下步骤选出两个变量来构造新的规划问题：
- 选出违反 KKT 条件最严重的样本点、以其对应的变量作为第一个变量
- 第二个变量的选取有一种比较繁复且高效的方法，但对于一个朴素的实现而言、第二个变量即使随机选取也无不可
将上述步骤选出的变量以外的变量固定、仅针对这两个变量进行最优化。易知此时问题转化为了求二次函数的极大值、从而能简单地得到解析解

这里仅简要说明一下 SVM 对偶算法中的 KKT 条件，详细的陈列则会放在相关数学理论中。具体而言、 $\alpha_{i}$ 及其对应样本 $(x_{i},y_{i})$ 的 KKT 条件为：

$\begin{align} \alpha_{i} = 0 &\Leftrightarrow y_{i}g\left( x_{i} \right) \geq 1 \\ 0 < \alpha_{i} < C &\Leftrightarrow y_{i}g\left( x_{i} \right) = 1 \\ \alpha_{i} = C &\Leftrightarrow y_{i}g\left( x_{i} \right) \leq 1 \end{align}$

所谓违反 KKT 条件最严重的样本点的定义也有许多种、其中一种简单有效的定义为：

计算“损失向量” $c = \left( c_{1},\ldots,c_{N} \right)^{T}$ 、其中： $c_{i} = \left\lbrack y_{i}g\left( x_{i} \right) - 1 \right\rbrack^{2}$
将损失向量复制三份（、、）并分情况将相应位置的损失置为 0。具体而言：
- 将 $\alpha_{i} > 0$ 或 $y_{i}g\left( x_{i} \right) \geq 1$ 对应的 $c_{i}^{\left( 1 \right)}$ 置为 0
- 将 $\alpha_{i} = 0$ 或 $\alpha_{i} = C$ 或 $y_{i}g\left( x_{i} \right) = 1$ 对应的 $c_{i}^{\left( 2 \right)}$ 置为 0
- 将 $\alpha_{i} < C$ 或 $y_{i}g\left( x_{i} \right) \leq 1$ 对应的 $c_{i}^{\left( 3 \right)}$ 置为 0
将三份损失向量相加并取损失最大的样本对应 $\alpha_i$ 的作为SMO的第一个变量、亦即： $i = \arg{\max_{i}{\left\{ c_{i}^{\left( 1 \right)} + c_{i}^{\left( 2 \right)} + c_{i}^{\left( 3 \right)}|i = 1,\ldots,N\right\}}}$

在后面 SVM 的朴素实现中、我们打算采用的正是这种定义