AdaBoost 算法

由前文的讨论可知，问题的关键主要在如下两点：

• 如何根据弱模型的表现更新训练集的权重
• 如何根据弱模型的表现决定弱模型的话语权

我们接下来就看看 AdaBoost 算法是怎样解决上述两个问题的。事实上，能够将这两个问题的解决方案有机地糅合在一起、正是 AdaBoost 的巧妙之处之一

AdaBoost 算法陈述

不失一般性、我们以二类分类问题来进行讨论，易知此时我们的弱模型、强模型和最终模型为弱分类器、强分类器和最终分类器。再不妨假设我们现在有的是一个二类分类的训练数据集：

$$D = \{\left( x_{1},y_{1} \right),\left( x_{2},y_{2} \right),\ldots,(x_{n},\ y_{n})\}$$

其中，每个样本点都是由实例$x_{i}$和类别$y_{i}$组成、且：

$$x_{i} \in X \subseteq \mathbb{R}^{n}\ ;y_{i} \in Y = \{ - 1,\ + 1\}$$

这里的$X$是样本空间、$Y$是类别空间。AdaBoost 会利用如下的步骤、从训练数据中训练出一系列的弱分类器、然后把这些弱分类器集成为一个强分类器：

1. 输入：训练数据集（包含 N 个数据）、弱学习算法及对应的弱分类器、迭代次数 M
2. 过程：
   1. 初始化训练数据的权值分布 $$W_{0} = (w_{01},\ldots,w_{0N})$$
   2. 对$k = 0,1,\ldots,\ M - 1$：
      1. 使用权值分布为$W_{k}$的训练数据集训练弱分类器 $$g_{k + 1}(x)$$：$$X \rightarrow \{ - 1,\ + 1\}$$
      2. 计算$g_{k + 1}(x)$在训练数据集上的加权错误率 $$e_{k + 1} = \sum_{i = 1}^{N}{w_{\text{ki}}I(g_{k + 1}\left( x_{i} \right) \neq y_{i})}$$
      3. 根据加权错误率计算$g_{k + 1}(x)$的“话语权” $$\alpha_{k + 1} = \frac{1}{2}\ln\frac{1 - e_{k + 1}}{e_{k + 1}}$$
      4. 根据$g_{k + 1}(x)$的表现更新训练数据集的权值分布：被$g_{k + 1}\left( x \right)$误分的样本（$y_{i}g_{k + 1}\left( x_{i} \right) < 0$的样本）要相对地（以$e^{\alpha_{k + 1}}$为比例地）增大其权重，反之则要（以$e^{- \alpha_{k + 1}}$为比例地）减少其权重 $$w_{k + 1,i} = \frac{w_{\text{ki}}}{Z_{k}} \cdot exp( - \alpha_{k + 1}y_{i}g_{k + 1}(x_{i}))$$ $$W_{k + 1} = (w_{k + 1,1},\ldots,w_{k + 1,N})$$ 这里的$Z_{k}$是规范化因子 $$Z_{k} = \sum_{i = 1}^{N}{w_{\text{ki}} \cdot exp( - \alpha_{k + 1}y_{i}g_{k + 1}(x_{i}))}$$ 它的作用是将$W_{k + 1}$归一化成为一个概率分布
   3. 加权集成弱分类器 $$f\left( x \right) = \sum_{k = 1}^{M}{\alpha_{k}g_{k}(x)}$$
3. 输出：最终分类器$g(x)$ $$g\left( x \right) = sign\left( f\left( x \right) \right) = \text{sign}\left( \sum_{k = 1}^{M}{\alpha_{k}g_{k}\left( x \right)} \right)$$

注意：2.2.2 步骤得到的加权错误率如果足够小的话，可以考虑提前停止训练，但这样做往往不是最合理的选择（这点会在后文进行模型性能分析时进行较详细的说明）

我们在分配弱分类器的话语权时用到了一个公式：$\alpha_{k + 1} = \frac{1}{2}\ln\frac{1 - e_{k + 1}}{e_{k + 1}}$。在该公式中，话语权$\alpha_{k + 1}$会随着加权错误率$e_{k + 1} \in \lbrack 0,\ 1\rbrack$的增大而减小。它们之间的函数关系如下图所示：

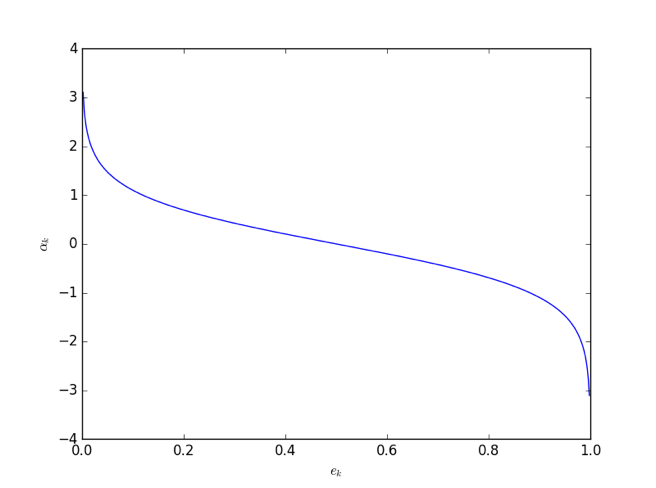
大多数情况我们训练出来的弱分类器的$e_{k} < 0.5$、对应着的是上图左半边的部分；不过即使我们的弱分类器非常差、以至于$e_{k} > 0.5$，由于此时$\alpha_{k} < 0$、亦即我们知道该分类器的表决应该反着来看、所以也不会出问题（有一种做法是如果训练到$e_{k} > 0.5$的话就停止训练，个人感觉也有道理）

弱模型的选择

看到这里，观众老爷们可能会产生这么一个疑问：如果我们不拘泥于对弱模型进行提升、转而对强模型或比较强的弱模型进行提升的话，会不会提升出更好的模型呢？从 Boosting 的思想来看、需要指出的是：用 Boosting 进行提升的弱模型的学习能力不宜太强，否则使用 Boosting 就没有太大的意义、甚至从原理上不太兼容。直观地说，Boosting 是为了让各个弱模型专注于“某一方面”、最后加权表决，如果使用了较强的弱模型，可能一个弱模型就包揽了好几方面，最后可能反而会模棱两可、起不到“提升”的效果。而且从迭代的角度来说，可以想象：如果使用较强弱模型的话，可能第一次产生的模型就已经达到“最优”、从而使得模型没有“提升空间”

注意：虽然笔者认为在 Boosting 中的弱模型就应该选择足够弱的模型，但确实亦有对强模型（如核 SVM）应用 Boosting 也很好的说法。详细而严谨的讨论会牵扯大量的数学理论、这里就不详细展开了

可能观众老爷们此时又会产生一个新的疑问：如果说 Boosting 中的弱模型不宜太强的话，是不是说 Bagging 中的个体模型也不宜太强呢？需要指出的是，虽然从理论上来说使用弱模型进行集成就已足以获得一个相当不错的最终模型，但使用较强的模型来进行集成从原理上是不太矛盾的。考虑到不同的场合，有时确实可以选用较强的模型来作为个体模型

那么所谓的不太强的弱模型大概是个什么东西呢？一个比较直观的例子就是限制层数的决策树。极端的情况就是限定它只能有一层、亦即上一章我们提到过的“决策树桩”，对应的进行了提升后的模型就是相当有名的提升树（Boosting Tree），它被认为是统计学习中性能最好的方法之一、既可以用来做分类也可以拿来做回归，是个相当强力的模型

AdaBoost 的实现

从之前的算法讲解其实可以看出，虽然 AdaBoost 算法本身很不平凡，但它给出的步骤都是相当便于实现的，基本上一个步骤就对应着 Python 里面的一行代码。在实现的过程中，困难之处可能主要在于如何让实现出来的 AdaBoost 框架易于扩展并具有方便调用的接口，而不在于实现算法本身。同时，为了能够更好地理解 AdaBoost 算法，我们需要对其性能作一系列的分析

由于 AdaBoost 是一个用于提升弱模型的算法，所以我们整体的实现思路大致是（不失一般性、我们先讨论二类分类问题）：

• 搭建 AdaBoost 框架
• 使用 sklearn 中的分类器对框架的正确性进行检验
• 使用前两章实现的分类器进行对比实验

所以我们要先把 AdaBoost 框架实现出来。为此，先来看 AdaBoost 框架的初始化步骤（其中_SKlearn是我对 sklearn 中的模型做了一定程度的拓展后的模型包）：

from math import log
# 导入我们之前实现的朴素贝叶斯模型和决策树模型
from b_NaiveBayes.Vectorized.MultinomialNB import MultinomialNB
from b_NaiveBayes.Vectorized.GaussianNB import GaussianNB
from c_CvDTree.Tree import *
from _SKlearn.NaiveBayes import *
from _SKlearn.Tree import *

class AdaBoost:
    # 弱分类器字典，如果想要测试新的弱分类器的话、只需将其加入该字典即可
    _weak_clf = {
        "SKMNB": SKMultinomialNB,
        "SKGNB": SKGaussianNB,
        "SKTree": SKTree,

        "MNB": MultinomialNB,
        "GNB": GaussianNB,
        "ID3": ID3Tree,
        "C45": C45Tree,
        "Cart": CartTree
    }
    """
        AdaBoost框架的朴素实现
        使用的弱分类器需要有如下两个方法：
            1) 'fit'      方法，它需要支持输入样本权重
            2) 'predict'  方法, 它用于返回预测的类别向量
        初始化结构
        self._clf：记录弱分类器名称的变量
        self._clfs：记录弱分类器的列表
        self._clfs_weights：记录弱分类器“话语权”的列表
    """
    def __init__(self):
        self._clf, self._clfs, self._clfs_weights = "", [], []

接下来就是训练和预测部分的代码：

def fit(self, x, y, sample_weight=None, clf=None, epoch=10, eps=1e-12, **kwargs):
    # 默认使用10个CART决策树桩作为弱分类器
    if clf is None or AdaBoost._weak_clf[clf] is None:
        clf = "Cart"
        kwargs = {"max_depth": 1}
    self._clf = clf
    if sample_weight is None:
        sample_weight = np.ones(len(y)) / len(y)
    else:
        sample_weight = np.array(sample_weight)
    # AdaBoost算法的主循环，epoch为迭代次数
    for _ in range(epoch):
        # 根据样本权重训练弱分类器
        tmp_clf = AdaBoost._weak_clf[clf](**kwargs)
        tmp_clf.fit(x, y, sample_weight)
        # 调用弱分类器的predict方法进行预测
        y_pred = tmp_clf.predict(x)
        # 计算加权错误率；考虑到数值稳定性，在边值情况加了一个小的常数
        em = min(max((y_pred != y).dot(self._sample_weight[:, None])[0], eps), 1 - eps)
        # 计算该弱分类器的“话语权”
        am = 0.5 * log(1 / em - 1)
        # 更新样本权重并利用deepcopy将该弱分类器记录在列表中
        sample_weight *= np.exp(-am * y * y_pred)
        sample_weight /= np.sum(sample_weight)
        self._clfs.append(deepcopy(tmp_clf))
        self._clfs_weights.append(am)

def predict(self, x):
    x = np.atleast_2d(x)
    rs = np.zeros(len(x))
    # 根据各个弱分类器的“话语权”进行决策
    for clf, am in zip(self._clfs, self._clfs_weights):
        rs += am * clf.predict(x)
    # 将预测值大于0的判为类别1，小于0的判为类别-1
    return np.sign(rs)