正如前文所说,在实现完 AdaBoost 框架后,我们需要先用 sklearn 中的分类器进行检验、然后再用我们前两章实现的模型进行对比实验。检验的步骤就不在这里详述(毕竟只是一些调试的活),我们在此仅展示在随机森林模型和经过检验的 AdaBoost 模型上进行的一系列的分析
直观起见,我们先采用二维的数据进行实验、并通过可视化来加深对随机森林和 AdaBoost 的理解,然后再用蘑菇数据集做比较贴近现实的实验。为讨论方便,我们一律采用决策树作为 AdaBoost 的弱分类器(亦即采用提升树模型进行讨论)、其强度可以通过调整其最深层数来控制。我们可以利用DataUtil类来生成或获取原始数据集,其完整代码可参见这里、生成数据集的代码则会在前三节分别放出
对于二维数据,我们拟打算使用三种数据集来进行评估:
- 随机数据集。该数据集主要用于直观地感受模型的分类能力
- 异或数据集。该数据集主要用于直观地理解:
- 集成模型正则化的能力
- 为何说 AdaBoost 不要选用分类能力太强的弱分类器
- 螺旋线数据集,主要用于直观认知随机森林和提升树的不足
随机数据集上的表现
生成随机数据集的代码如下:
|
|
随机森林在随机数据集上的表现如下图所示:
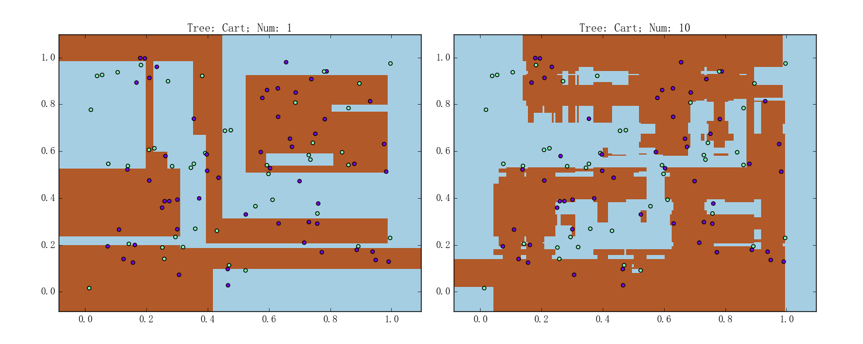
左图为包含 1 棵 CART 树的随机森林,准确率为 78.0%;右图则为包含 10 棵 CART 树的随机森林,准确率为 93.0%。如果将树的数量继续往上抬、达到 100%准确率并非难事。比如,包含 5 0棵 CART 树的随机森林的表现如下图所示:
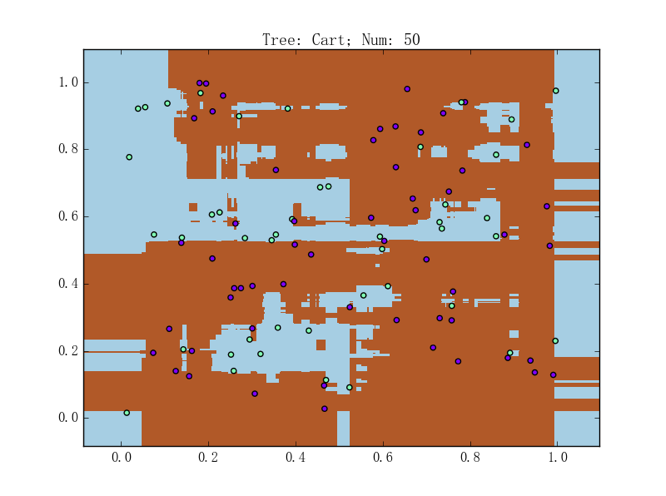
提升树(弱模型为决策树的 AdaBoost)在随机数据集上的表现如下图所示:
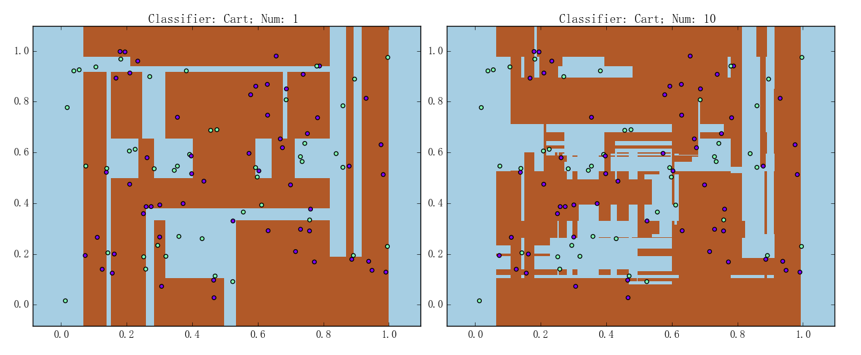
左图为包含 1 棵 CART 树的 AdaBoost,准确率为 93.0%;右图则为包含 10 棵 CART 树的 AdaBoost,准确率为 99.0%
异或数据集上的表现
这里主要是想说明随机森林和提升树正则化的效果。从直观上来说,由于随机森林的理论基础是 Bootstrap、所以自然是包含越多树越好;至于 AdaBoost,可以想象它会对难以分类的数据特别在意、从而导致如下两种可能的结果:
- 太过注重噪声,导致过拟合
- 专注于类似于下一个系列要讲的 SVM 中的“支持向量”,从而达到正则化
事实上正如之前提到过的,即使 AdaBoost 在某一步迭代时、所得的模型在训练集上的加权错误率已经达到了 0,继续进行训练仍然可以使模型进一步提升(因为单个模型的正确率没有那么高、从而能使模型继续专注于“支持向量”。所谓支持向量、可以暂时直观地理解为“非常重要的”样本)。为说明这一点,我们可以比较同一数据集上、同样使用最深层数为 3 层的决策树作为弱分类器时、两种不同训练策略在异或数据集上的表现。为了比较准确地衡量正则化能力,我们需要进行交叉验证。、
生成异或数据集的代码如下:
|
|
随机森林在异或数据集上的表现如下图所示:
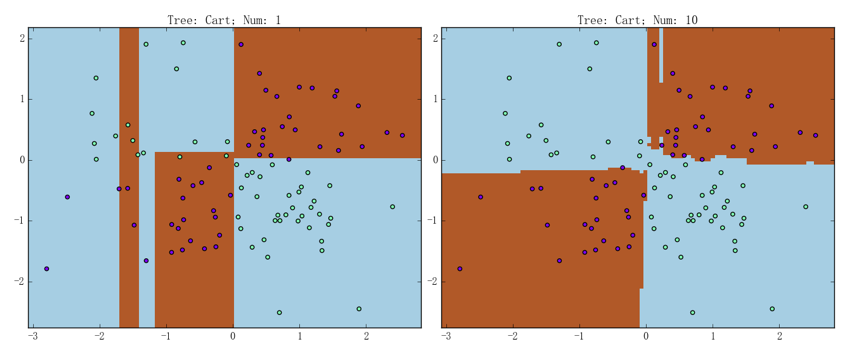
注意:该异或数据集和上一章用到的异或数据集是同一个数据集,感兴趣的读者可以进行一些对比
左图为包含 1 棵 CART 树的随机森林,准确率为 93.0%;右图则为包含 10 棵 CART 树的随机森林,准确率为 98.0%。虽说右图中随机森林的表现已经足够好,由前文讨论可知、我们应该尝试训练一个更复杂的随机森林来看看其正则化能力。比如,包含 1000 棵 CART 树的随机森林的表现如下图所示:
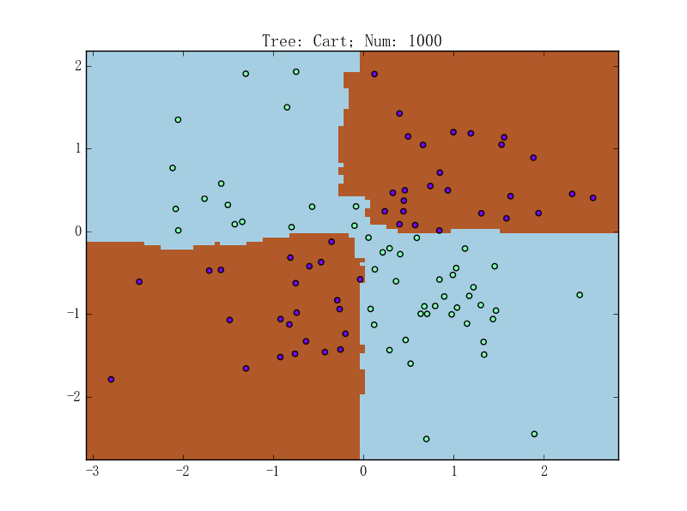
仔细观察决策边界,可以发现它会倾向于画在使得样本和边界“间隔较大”的地方。关于“间隔”的详细讨论会放在下一个系列,这里只需直观地感受一下即可
对于提升树,首先看一下不提前停止训练时的表现。为更好地说明问题,这里我们换了一个异或数据集来进行分析:
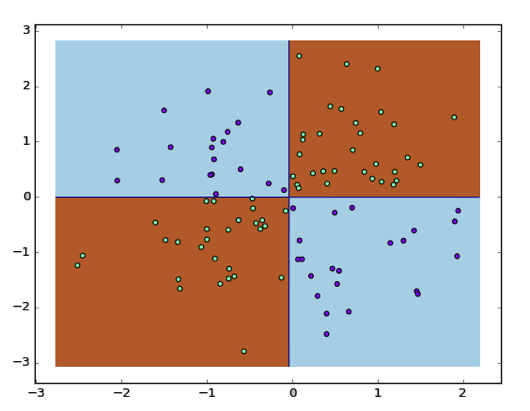
此时在测试数据集上的正确率为 97.0%。然后看当模型在训练集上错误率足够小就马上停止训练时的表现:
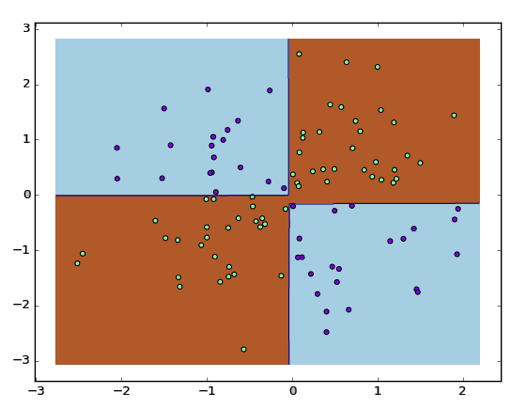
此时在测试数据集上的正确率为 94.0%
当然,正如前面所说,事实上确实有论文(G. Ratsch et al. ML, 2001)给出了 AdaBoost 会很快就过拟合的例子。但总体而言,笔者认为 AdaBoost 在正则化这一方面的表现还是相当优异的
由前面的诸多讨论可以得知,AdaBoost 的正则化能力是来源于各个弱分类器的“分而治之”,那么如果使用分类能力强的弱分类器会有什么结果呢?下面就放出当选用不限制层数的决策树作为弱模型的、异或数据集上的表现,相信会带来很好的直观:
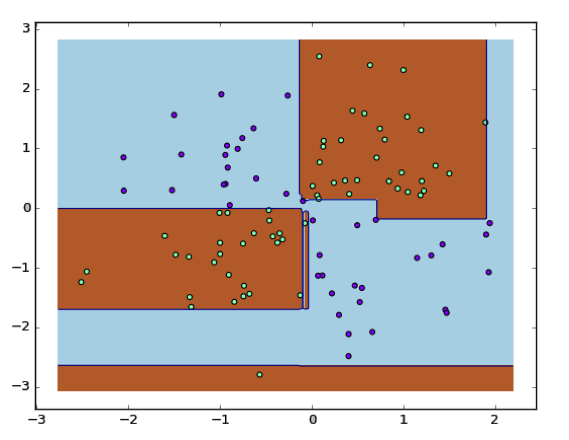
此时在测试数据集上的正确率为 90.0%。值得一提的是,用单独的决策树做出来的效果和上图的效果几乎完全一致。换句话说、此时使用 AdaBoost 没有太大的意义
螺旋数据集上的表现
随机森林和提升树虽然确实都相当强大、但它同样具有其基本组成单元——决策树所具有的某些缺点。比如说,它们在处理连续性比较强的数据时可能会有些吃力、因为它们的决策边界一般而言都是“不太光滑”的。下面我们就统一使用个体决策树不做层数限制的随机森林和提升树以及螺旋线数据集作为样例来进行说明
生成螺旋数据集的代码如下:
|
|
随机森林和提升树在其上的表现分别如下两张图所示:
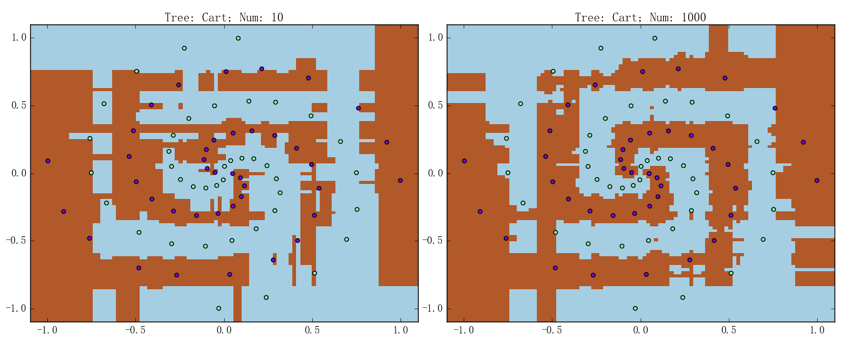
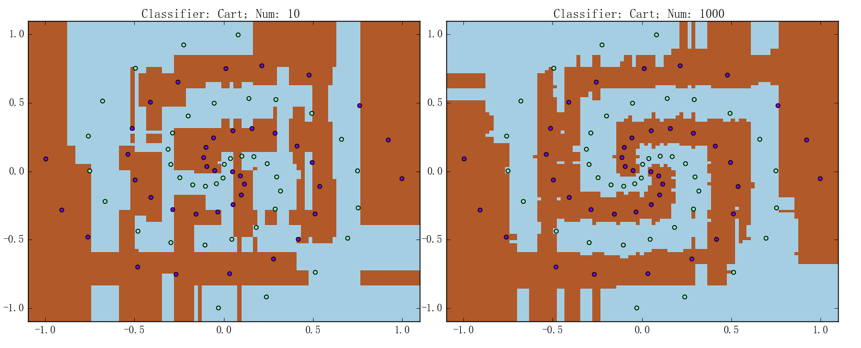
上面两组图的左边都是包含 10 棵 CART 树的模型、右边都是包含 1000 棵 CART 树的模型,准确率则都是为 100.0%。可以看到,虽然它们都确实能够将大致的趋势给描述出来、但是决策边界相对而言都是“直来直去”的,这一点要比支持向量机、神经网络等模型的训练出来的结果要差不少。总之,决策树那使用二类问题的解决方案来处理连续型特征的做法、导致了随机森林和提升树在处理连续特征上的一些不足
蘑菇数据集上的表现
目前为止我们对二维数据上的测试做了比较详尽的说明,接下来我们不妨拿蘑菇数据集来测试一下我们的模型在真实数据下的表现;鉴于该数据集比较简单、我们只使用 100 个样本进行训练并用剩余的 8000 多个样本进行测试。为了直观感受模型的分类能力,我们可以画出当个体模型为 CART 决策树桩时、两种集成模型在测试集上的准确率随训练迭代次数变化而变化的曲线:
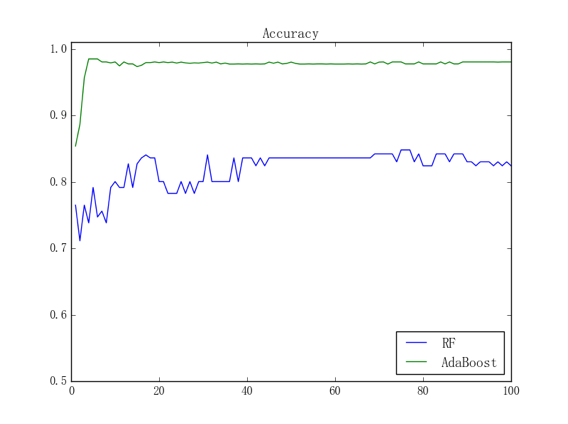
其中蓝线是随机森林的训练曲线、绿线是提升树的训练曲线。这个结果是符合直观的,毕竟从个体模型来讲,引入了随机性的、随机森林中的决策树桩要比提升树中正常的决策树桩要弱,所以提升树的收敛速度理应比随机森林的要快;此外,由于随机森林和提升树相比、受个体模型分类能力的影响更大、我们采用的又是 CART 决策树桩这种相当弱的个体模型,所以随机森林收敛后的表现也要比提升树收敛后的表现要差
不过需要指出的是,当我们取消个体 CART 决策树的层数限制时,虽然随机森林的收敛速度仍会比提升树的收敛速度慢、但是收敛后的表现却很有可能比提升树收敛后的表现要好。这是因为取消了层数限制的决策树是相当强力的模型,而且:
- 一方面正如刚刚所说的,随机森林受个体模型的分类能力影响较大、所以取消个体树的层数限制后、随机森林的分类能力自然大大增强
- 另一方面则如之前所讨论的,具有较强分类能力的个体模型与 AdaBoost 的原理可能不太兼容,这就使得 AdaBoost 本身的优势被抑制了
取消层数限制后重复上述实验,此时两种集成模型的训练曲线如下图所示:
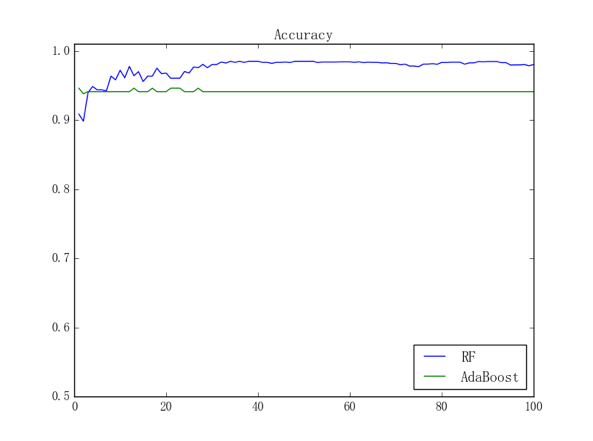
可能观众老爷们已经发现,取消层数限制后的提升树似乎还没有取消限制之前的提升树的表现好;事实上,由于我们只用了 100 个样本来进行训练,所以容易想象、取消限制后的提升树将会产生比较严重的过拟合。可以把取消层数限制前后的训练曲线放在一起来进行直观对比,结果如下图所示:
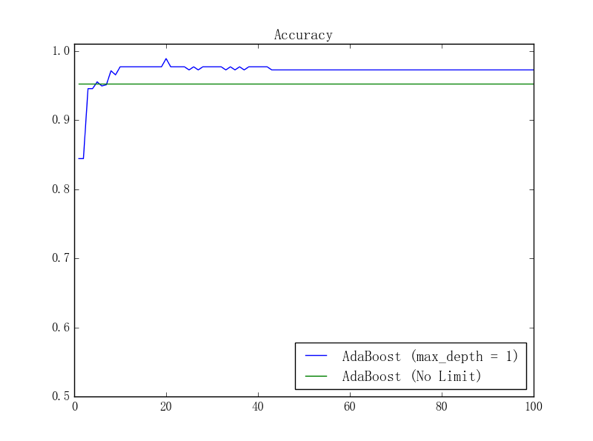
其中蓝线是个体模型为 CART 决策树桩时的训练曲线、绿线是个体模型为正常 CART 决策树时的训练曲线

