朴素贝叶斯综述

发表于 | 分类于

朴素贝叶斯（Naive Bayes）是贝叶斯分类器的一种，而后者是一个相当宽泛的定义，它背后的数学理论根基是相当出名的贝叶斯决策论（Bayesian Decision Theory）。贝叶斯决策论和传统的统计学理论有着区别，其中最不可调和的就是它们各自关于概率的定义。因此，使用了贝叶斯决策论作为基石的贝叶斯分类器，在各个机器学习算法所导出的分类器中也算是比较标新立异的存在

由于朴素贝叶斯这一块能够扯到的理论还是相当多的，我们会把内容分成数学理论部分与程序实现部分，观众老爷们可以按需阅读 ( σ’ω’)σ

以下是目录：

涉及到的理论

首先无法避开的自然就是贝叶斯决策论了，然而我本人对其可以说只有一个入门级别的理解、所以相应的说明更多只能起到一种抛砖引玉的作用

然后是参数估计，这一部分是比较基础的知识，但真要做起来还是相当繁琐的

至于其余的贝叶斯分类器，为了将重点放在朴素贝叶斯，我们仅会在最后进行一些简要的介绍，相关的实现和更深层次的推导等等则不会进行说明（主要是我也不咋懂）

程序实现的大体思路

  • 离散型朴素贝叶斯的实现围绕着 Numpy 中的bincount方法展开
  • 连续型朴素贝叶斯的关键在于极大似然估计
  • 混合型朴素贝叶斯则是以上两者的各种结合

程序运行的结果预览

本来要说的话、朴素贝叶斯是很难让人直观地看出来它干了什么的，不过聪明而机智的我想出了一个方法：把中间产生的那些条件概率可视化出来不就可以蒙混过关了！

于是我们的朴素贝叶斯模型可以生成类似于这样的图：

离散型朴素贝叶斯的可视化 连续型朴素贝叶斯的可视化

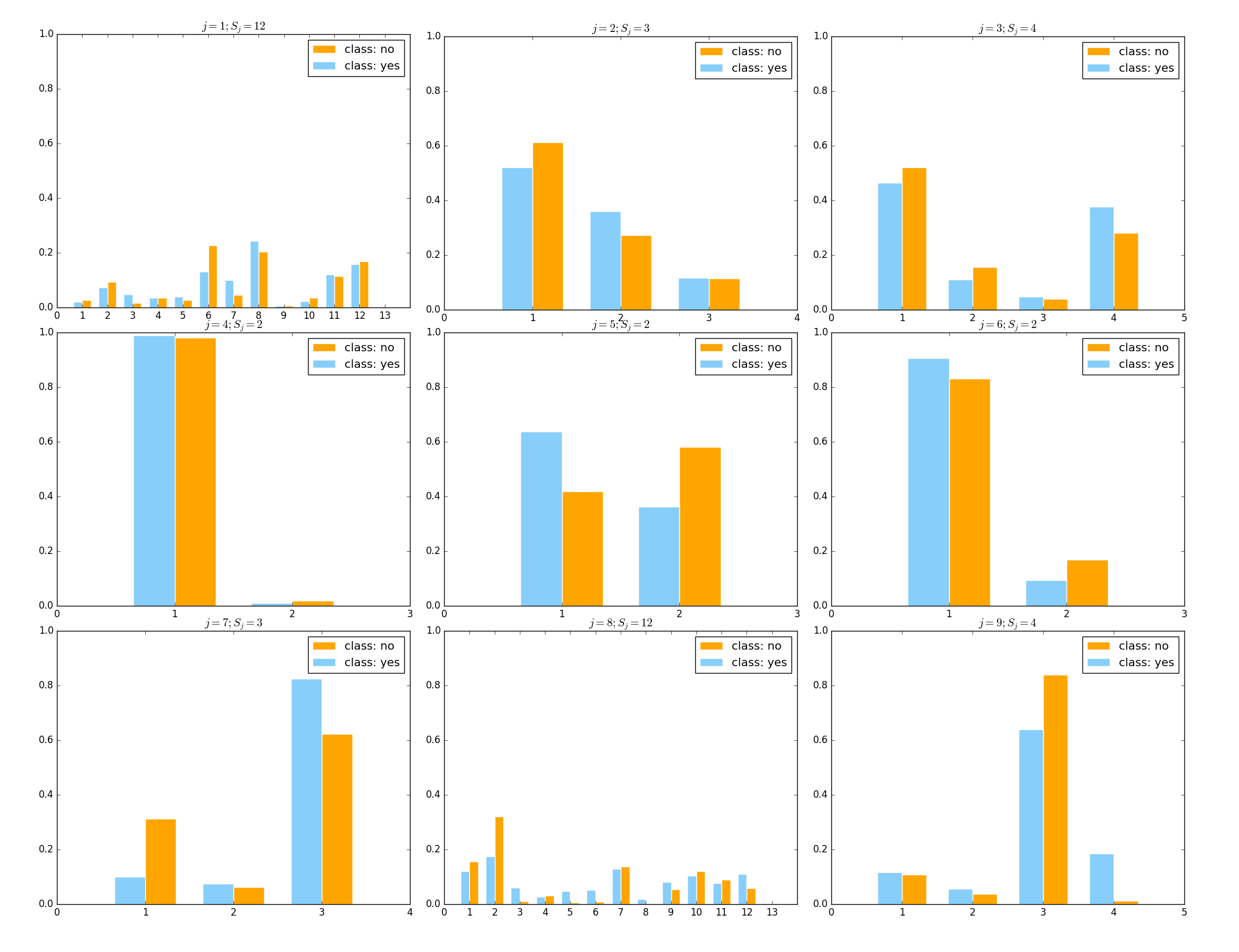
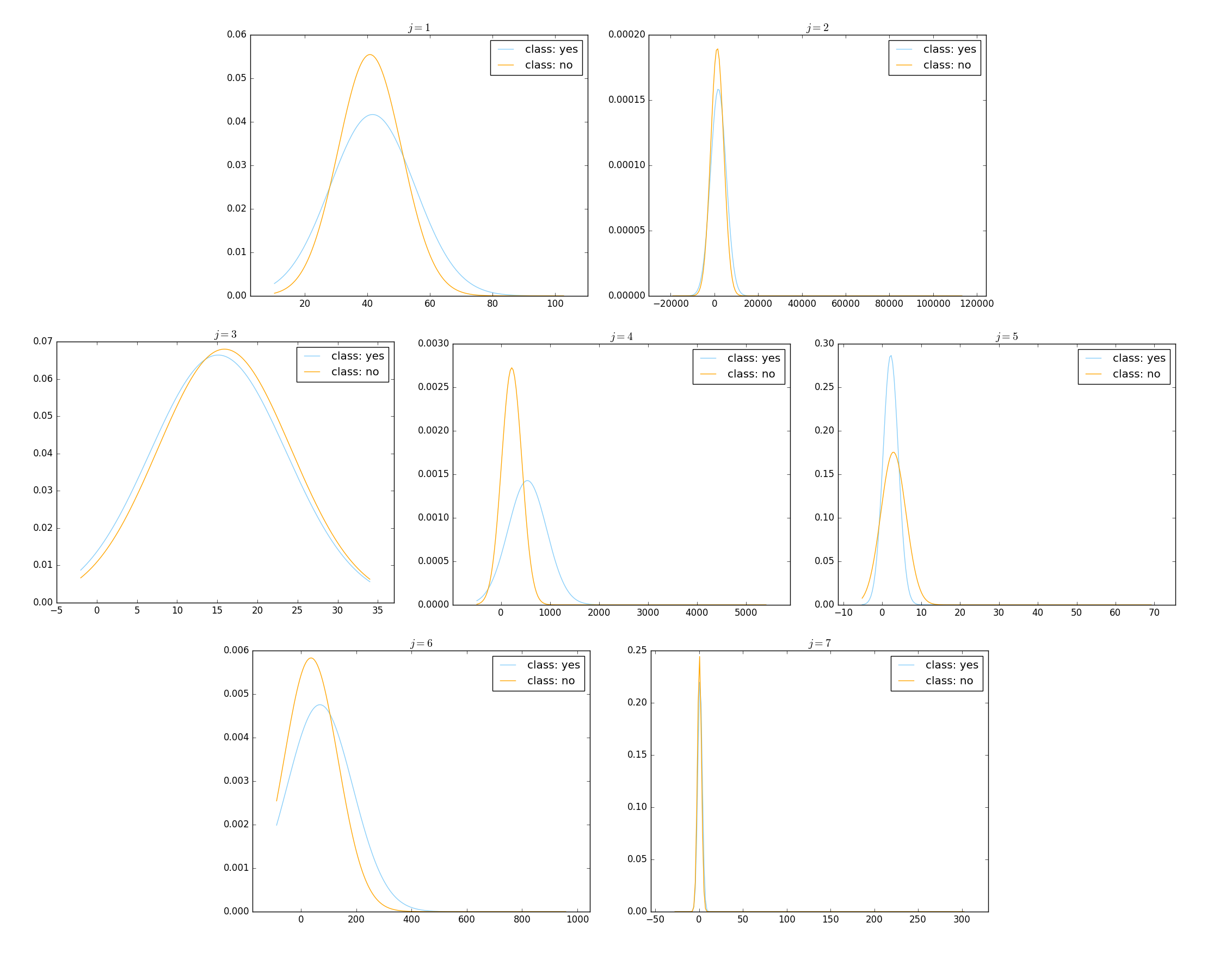
注意：这些图是分开生成的，是我用画图软件（很傻地）很辛苦地把它们拼在一起的

以上 16 张图（离散型特征 9 张、连续型特征 7 张）对应着一个有 16 个特征的、UCI 上的“银行业务数据集”，完整的原始数据集可以参见这里

然后我们实现的朴素贝叶斯模型的最大特点就是：无需对数据进行太多预处理。还是以银行业务数据集为例，它每个样本大概长下面这样：

1
58, management, married, tertiary, no, 2143, yes, no, unknown, 5, may, 261, 1, -1, 0, unknown

我们可以直接把它输进模型而无需做其它多余的工作。当然、这是建立在我们自己写一套数值化数据的方法的基础上的，关于这个数值化数据的实现可以参见这里

观众老爷们能赏个脸么 ( σ'ω')σ