本文首先简要地说明一下决策树生成算法背后的数学基础和思想、然后再叙述具体的算法。往大了说、决策树的生成可以算是信息论的一个应用,但它其实只用到了信息论中一小部分的思想。不过,先对信息论有个概括性的认知还是有必要的、因为这样我们就可以有个更宽的视野
信息论简介
(注:本节有许多内容节选、修改、总结自维基百科)
被誉为信息论创始人的是克劳德·艾尔伍德·香农(Claude Elwood Shannon,1916.4.30-2001.2.26),他是美国数学家、电子工程师和密码学家,是密歇根大学学士、麻省理工学院博士。他在 1948 年发表的划时代的论文——“通信的数学原理”奠定了现代信息论的基础
信息论(Information Theory)涉及的领域相当多,包括但不限于信息的量化、存储和通信、统计推断、自然语言处理、密码学等等。信息论的主要内容可以类比人类最广泛的交流手段——语言来阐述。一种简洁的语言(以英语为例)通常有如下两个重要特点:
- 最常用的一些词汇(比如“a”、“the”、“I”)应该要比相对而言不太常用的词(比如“Python”、“Machine”、“Learning”)要短一些
- 如果句子的某一部分被漏听或者由于噪声干扰(比如身处闹市)而被误听,听者应该仍然可以抓住句子的大概意思
其中第二点被称作为“鲁棒性(Robustness)”。如果把电子通信系统比作一种语言的话,这种鲁棒性(Robustness)不可或缺。信息论的基本研究课题是信源编码和信道编码(通俗一点来讲就是怎么发出信息和怎么传递信息),将鲁棒性引入通信正是通过其中的信道编码来完成的,由此可见信息论的重要性
注意这些内容同消息的重要性之间是毫不相干的。例如,像“你好;再见”这样的话语和像“救命”这样的紧急请求,在说起来或写起来所花的时间是差不多的,然而明显后者更重要也更有意义。信息论却不会考虑一段消息的重要性或内在意义,因为这些属于信息的质量的问题而不是信息量和可读性方面上的问题,后者只是由概率这一因素单独决定的
既然我们我们关注的是信息量,我们就需要有一个度量方法。决策树生成算法背后的思想正是利用该度量方法来衡量一种“数据划分”的优劣、从而生成一个“判定序列”。具体而言,它会不断地寻找数据的划分方法、使得在该划分下我们能够获得的信息量最大(更详细的叙述会在后文给出)
不确定性
在决策树的生成中,获得的信息量的度量方法是从反方向来定义的:若一种划分能使数据的“不确定性”减少得越多、就意味着该划分能获得越多信息。这是很符合直观的,关键问题就在于应该如何度量数据的不确定性(或说不纯度,Impurity)。常见的度量标准有两个:信息熵(Entropy)和基尼系数(Gini Index),接下来我们就说说它们的定义和性质
信息熵
先来看看它的公式:
对于具体的、随机变量生成的数据集而言,在实际操作中通常会利用经验熵来估计真正的信息熵:
这里假设随机变量的取值空间为,表示取的概率:;代表由随机变量中类别为的样本的个数、代表的总样本个数(亦即)。可以看到,经验公式背后的思想其实就是“频率估计概率”
通常来说,公式中对数的底会取为 2、此时信息熵的单位叫作比特(bit);如果把底取为(亦即取自然对数)的话,的单位就称作纳特(nat)
接下来说明为何上式能够度量数据的不确定性。可以证明(详细推导可参见相关数学理论),当:
时,达到最大值、亦即。由于,上式即意味着随机变量取每一个类的概率都是一样的、亦即完全没有规律可循,想要预测它的取值只能靠运气。换句话说,由生成出来的数据的不确定性是在取值空间为、样本数为 N 的数据中最大的(想象预测 N 次正 K 面体骰子的结果)
我们的目的是想让的不确定性减小、亦即想让变得有规律以方便我们预测。稍微严谨地来说,就是取某个类的概率特别大、取其它类的概率都特别小。极端的例子自然就是存在某个、使得、、亦即y生成的样本总属于类。带入的定义式,可以发现此时、亦即生成的样本没有不确定性
注意:由于、所以认为
特殊的情况就是二类问题、亦即的情况。先不妨设只取 0、1 二值,再设:
那么此时的信息熵即为:
由此可得随变化的函数曲线。底为 2 时函数图像如下图所示:
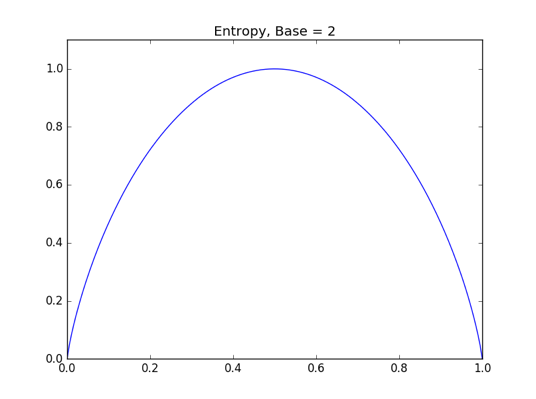
如前文所述,在时取得最大值 1。底为时函数图像则如下图所示:
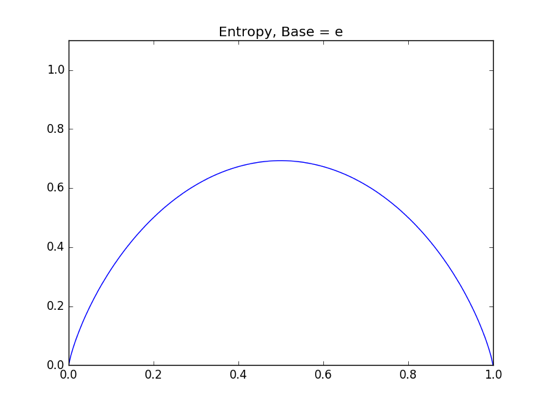
虽然最大值仍在时取得,但是此时仅有 0.693()左右
如果对上述二类问题稍作推广:、其中、都是一个集合,那么此时信息熵的定义式即为:
且易知:
如无特殊说明,今后谈及二类问题时讨论的范围都包括推广后的二类问题。
以上的叙述说明了,越乱意味着越大、越有规律意味着越小,亦即确实可以作为不确定性的度量标准
基尼系数
基尼系数的定义会更简洁一些:
同样可以利用经验基尼系数来进行估计:
以及同样可以证明,当
时,取得最大值;当存在使得时、。特别地、当时,可以导出:
此时的函数图像如下图所示:
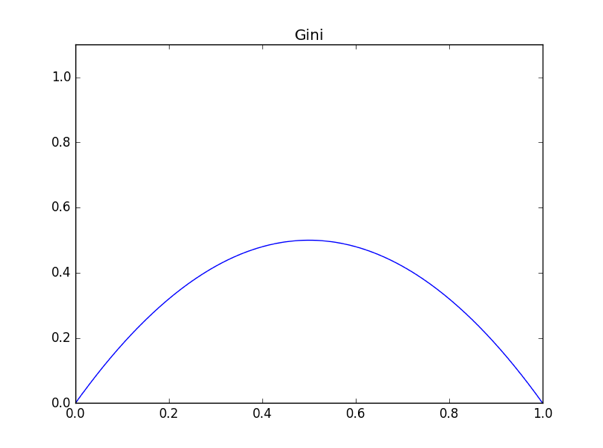
虽然最大值仍在时取得,但是此时仅有 0.5。我们同样可以对二类问题进行推广、此时有:
且
以上的叙述说明了也可以用来度量不确定性
信息的增益
在定义完不确定性的度量标准之后,我们就可以看看什么叫“获得信息”、亦即信息的增益了。从直观上来说,信息的增益是针对随机变量和描述该变量的特征来定义的,此时数据集,其中是描述的特征向量、n 则是特征个数。我们可以先研究单一特征的情况():不妨设该特征叫、数据集;此时所谓信息的增益,反映的就是特征所能给我们带来的关于的“信息量”的大小
可以引入条件熵的概念来定义信息的增益,它同样有着比较好的直观:
- 所谓条件熵,就是根据特征的不同取值对进行限制后,先对这些被限制的分别计算信息熵、再把这些信息熵(一共有 m 个)根据特征取值本身的概率加权求和、从而得到总的条件熵。换句话说,条件熵是由被不同取值限制的各个部分的的不确定性以取值本身的概率作为权重加总得到的
所以,条件熵越小、意味着被限制后的总的不确定性越小、从而意味着A更能够帮助我们做出决策
接下来就是数学定义:
其中
同样可以用经验条件熵来估计真正的条件熵:
这里的表示在限制下的数据集。通常可以记中的样本满足,亦即:
而公式中的则代表着中第 k 类样本的个数
从条件熵的直观含义,信息的增益就可以自然地定义为:
这里的常被称为互信息(Mutual
Information),决策树中的 ID3 算法即是利用它来作为特征选取的标准的(相关定义会在后文给出)。但是,如果简单地以作为标准的话,会存在偏向于选择取值较多的特征、也就是 m 比较大的特征的问题。我们仍然可以从直观上去理解为什么会偏向于选取 m 较大的特征以及为什么这样做是不尽合理的:
- 我们希望得到的决策树应该是比较深(又不会太深)的决策树,从而它可以基于多个方面而不是片面地根据某些特征来判断
- 如果单纯以作为标准,由于的直观意义是被划分后不确定性的减少量,可想而知,当的取值很多时,会被划分成很多份、于是其不确定性自然会减少很多、从而 ID3 算法会倾向于选择作为划分依据。但如果这样做的话,可以想象、我们最终得到的决策树将会是一颗很胖很矮的决策树,这并不是我们想要的
为解决该问题、我们可以给 m 一个惩罚,由此我们可以得到信息增益比(Information
Gain Ratio)的概念,该概念对应着 C4.5 算法:
其中是关于的熵,它的定义为:
同样可以用经验熵来进行估计:
该定义式和信息熵的定义式很像,它们的性质也有相通之处
需要指出的是,只需要类比上述的过程、我们同样可以使用基尼系数来定义信息的增益。具体而言,我们可以先定义条件基尼系数:
其中
同样可以用经验条件基尼系数来进行估计:
信息的增益则自然地定义为(不妨称之为“基尼增益”):
决策树算法中的CART算法通常会应用这种定义

