从感知机到多层感知机

“神经网络”这个概念本身其实是一个庞大的交叉学科，而在机器学习领域里、“神经网络”则是“人工神经网络（Artificial Neural Network）”的简称。顾名思义，本系列所将介绍的神经网络模型多少借鉴了神经生理学关于神经网络的研究、并尝试通过数学建模来描述机器智能，这也正是为何许多机器学习相关书籍对神经网络的介绍都会从“真正的”神经网络开始（比如介绍细胞体、树突、轴突和突触之类的）。然而个人认为，直到目前为止、我们一般应用的神经网络结构其实和真正的神经网络之结构之间的差距还是相当大的；如果按照生物学意义上的神经网络来理解人工神经网络的话，虽说从直观上来说可能更加易懂、但在逻辑和原理的层面上反而会造成混淆

为此我们就跳过“老生常谈”般的、介绍生物学意义上的神经网络的部分并直接把数学建模后的结果进行说明：近现代最常用的NN模型其实脱胎于 1943 年由 W. S. McCulloch 和 W. H. Pitts 提出的 McCulloch-Pitts 神经元模型（常简称为 M-P 神经元模型），它针对单个的神经元进行了数学建模。具体而言、M-P 模型是具有如下三个功能的模型：

能够接收 n 个 M-P 模型传递过来的信号
能够在信号的传递过程中为信号分配权重
能够将得到的信号进行汇总、变换并输出

可以通过下图来直观认知 M-P 模型的结构：

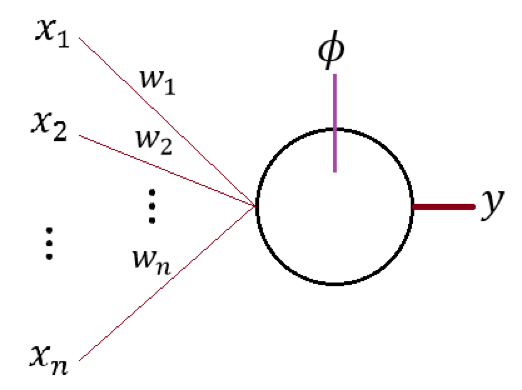
图中的 $x_{1},\ldots,x_{n}$ 即为 n 个 M-P 模型的输出信号、 $w_{1},\ldots,w_{n}$ 即为这 n 个信号对应的权值； $\phi$ 即为所示神经元对输入信号的变换函数、y 即为模型的输出。一般而言我们可以把 y 写成：

$y = \phi\left( \sum_{i = 1}^{n}{w_{i}x_{i}} + b \right)$

其中 b 为神经元对输入信号的“平移”。我们通常会称 $\phi$ 为激活函数而称 b 为偏置量，有关它们的详细讨论会在前向传导算法中进行、这里就暂时先按下不表

有了 M-P 神经元模型的话、基于它来定义神经网络似乎就不是一件困难的事了；事实上、只需要把许多 M-P 神经元按照一定的层次结构进行连接即可。一个非常自然的想法就是构建一个有向无环图（DAG 图），其输入节点和输出节点视具体问题而定。比如若想通过三维的输入来得到二维的输出、我们可以简单地以 M-P 模型为有向无环图中的节点来构造一个如下图所示的有向无环图：

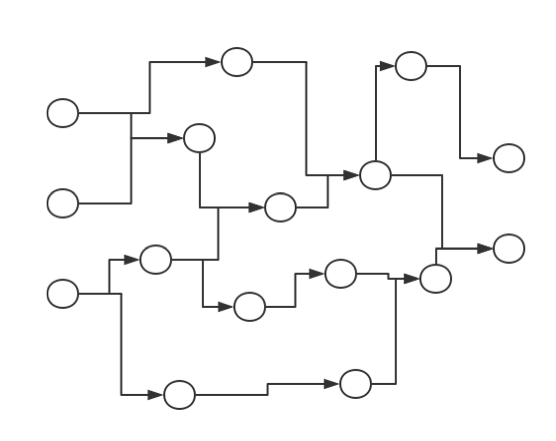
如果人工神经网络模型真的能够对任意 DAG 图都能进行高效训练的话、那么说它和真正的神经网络能够互相类比可能也不算夸张；然而遗憾的是，由于现在我们对矩阵运算的依赖程度很大（因为矩阵运算是被高度优化了的），所以目前主流的神经网络模型结构基本都是一类及其特殊的 DAG 图。具体而言、主流人工神经网络模型是以“层（Layer）”（而不是以“节点”）为基本单位的，其结构大致如下图所示：

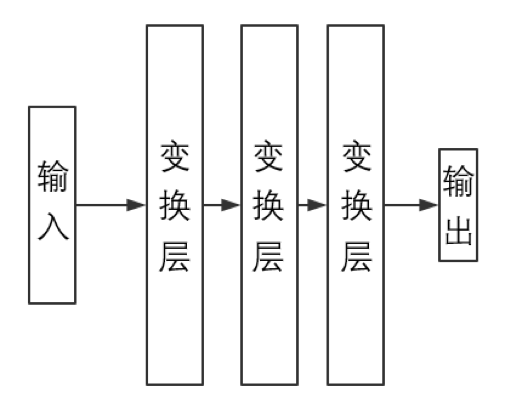
其中，输入（层）、变换层和输出（层）都可以想象为是若干 M-P 神经元“排列在一起”而组成的“神经层”、从而整张神经网络即为由若干神经层“堆叠而成”的一个结构。不难想象在这种情况下、同一层中的所有 M-P 神经元会共享激活函数 $\phi$ 和偏置量 b，所以通常我们会针对层结构定义 $\phi$ 和 b 而不是针对单个的神经元定义 $\phi$ 和 b

如果确实想以“节点”为基本单位、那么上图所示结构可以化为如下图所示的模型：

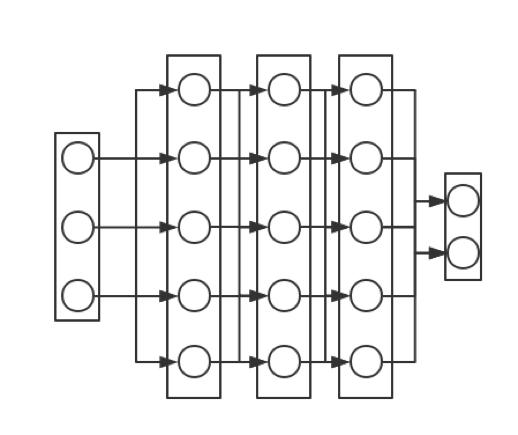
其中除了输出层外、当前层的每个节点都会出来一个箭头指向下一层中的每个节点，这也正是当前层将信号传输给下一层的方式。容易想象当没有变换层时、人工神经网络就会“退化”成我们上个系列中讲过的感知机。事实上可以将第一张图所示的神经元看作是只有一个神经元的输出层并令 $\phi$ 为恒同映射、亦即：

$\phi(x) = x,\ \ \forall x\mathbb{\in R}$

那么就有

$y = \sum_{i = 1}^{n}{w_{i}x_{i}} + b = w \cdot x + b$

其中

$w = \left( w_{1},\ldots,w_{n} \right)^{T},\ \ x = \left( x_{1},\ldots,x_{n} \right)^{T}$

可以看出上式即为感知机的决策公式。由此可见、这种主流人工神经网络结构其实可以称为多层感知机模型（Multi-Layer Perceptron，常简称为 MLP），本章所说的神经网络所代指的也正是 MLP 模型。它的工作原理是直观的：

输入层和输出层即为整个模型的入口和出口
变换层则会把上一层的输出当成输入、经过一番内部处理后把输出传给下一层

所以问题的关键就在于层结构（Layer）的搭建上。不过在着手实现它之前、了解它具体需要做哪些工作是有必要的。如果往简单去说、神经网络算法其实只包含如下三个部分：

通过将输入进行一层一层的变换来得到输出
通过输出与真值的比较得到损失函数的梯度
利用得到的这个梯度来更新模型的各个参数

其中前两个部分相关的内容会在下两节进行简单的说明、第三个部分相关内容的简要叙述则会放在第四节。注意到第二个部分中提到了“损失函数”的概念；在我们将要实现的神经网络模型中、我们会将损失作为一个单独的层结构跟在输出层后面。换句话说、一个完整的神经网络模型将如下图所示：

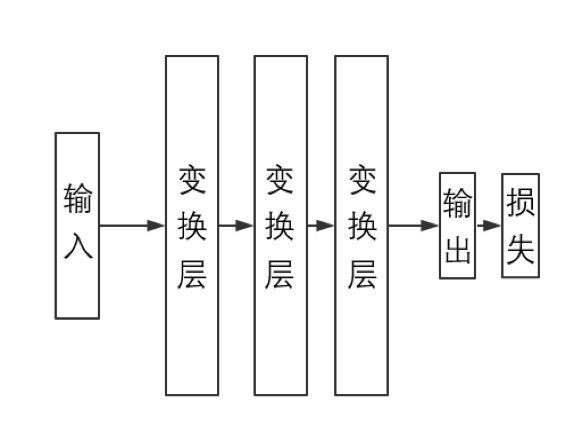
注意：今后章节中出现的各个数学算式中的元素如果不带下标的话、一般而言都代指向量或者矩阵而不是标量；为使文章结构连贯，我们不会一一说明哪些是标量、哪些是向量而哪些是矩阵，但是通过上下文和具体的算法、相关叙述应该是不会引起歧义的

此外需要指出的是，由于损失层 CostLayer 只是为了实现的便利性而存在的结构、从数学的角度来讲它是不必抽出来作为一个独立个体的。因此我们有时会在叙述数学相关问题时会隐去 CostLayer