“大数据”下的网络结构

发表于 | 分类于

本文标题处的“大数据”打上了引号，是因为我们所要讨论的不是当今十分火热的、真正的大数据问题、而是讨论当问题规模“相当大”时应该如何处理。我们虽然在上篇文章中实现了一个切实可用的神经网络、但它确实显得过于朴实。本文会说明如何在这个朴实模型的基础上进行拓展，这些拓展的手法不单适用于神经网络、还适用于诸多旨在解决现实生活中规模相对较大的任务的模型

分批（Batch）的思想

回忆上一节实现的朴素神经网络中的fit方法、可以发现每次迭代时我们都只会用整个训练集进行一次参数的更新；以 Vanilla Update 为例的话、我们进行的就是 BGD 而非 MBGD。在数据量比较大时，姑且不论 MBGD 算法和 BGD 算法本身孰优孰劣，单从内存问题来看、BGD 就不是一个可以接受的做法。因此与 MBGD 算法的思想类似、我们需要将训练集“分批（Batch）”进行训练

同样的道理，目前我们做预测时是将整个预测数据集扔给模型让它做前传算法的。当数据量比较大时、这样做显然也会引发内存不足的问题，为此我们需要分 Batch 进行前向传导并在最后做一个整合

总之在数据量变大的情况下、我们要时刻有着分 Batch 的思想。先来看看如何在训练过程中引入 Batch（以下代码需定义在fit方法中的相关位置、仅写出关键部分）：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
# 得到总样本数
train_len = len(x)
# 得到单个Batch中的样本数，其中batch_size是传进来的参数
batch_size = min(batch_size, train_len)
# 先判断是否有必要分Batch；若Batch中的样本数多于总样本数、自然没有必要分Batch
do_random_batch = train_len >= batch_size
# 算出需要分多少次Batch
train_repeat = int(train_len / batch_size) + 1
# 训练的主循环
for counter in range(epoch):
    # 进行train_repeat次子迭代、每次子迭代中会利用一个Batch来训练模型
    for _ in range(train_repeat):
        if do_random_batch:
            # np.random.choice(n, m)：随机从[0,1,...,n-1]中选出m个数
            batch = np.random.choice(train_len, batch_size)
            x_batch, y_batch = x_train[batch], y_train[batch]
        else:
            x_batch, y_batch = x_train, y_train
        self._w_optimizer.update()
        self._b_optimizer.update()
        _activations = self._get_activations(x_batch)
        _deltas = [self._layers[-1].bp_first(y_batch, _activations[-1])]
        for i in range(-1, -len(_activations), -1):
            _deltas.append(
                self._layers[i - 1].bp(_activations[i - 1], self._weights[i], _deltas[-1])
            )
        for i in range(layer_width - 1, 0, -1):
            self._opt(i, _activations[i - 1], _deltas[layer_width - i - 1])
        self._opt(0, x_batch, _deltas[-1])

然后是在预测过程中引入 Batch，实现的方法有两种：一种是比较常见的按个数分 Batch、一种是我们打算采用的按数据大小分 Batch。换句话说：

  • 常见的做法是在每个 Batch 中放 k 个数据
  • 我们的做法是在每个 Batch 中放 m 个数据、它们一共大概包含 N 个数字

其中常见做法有一个显而易见的缺点：如果单个数据很庞大的话、这样做可能还是会引发内存不足的问题。接下来就看看我们的做法相对应的具体实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
# 参数batch_size即为N
def _get_prediction(self, x, batch_size=1e6):
    # 计算Batch中的数据个数m、默认
    single_batch = int(batch_size / np.prod(x.shape[1:]))
    # 如果单个样本的数据量比N还大、那么将m设为1
    if not single_batch:
        single_batch = 1
    # 如果m大于样本总数、直接将所有样本输入前向传导算法即可
    if single_batch >= len(x):
        return self._get_activations(x).pop()
    # 否则、计算需要重复调用前向传导算法的次数
    epoch = int(len(x) / single_batch)
    if not len(x) % single_batch:
        epoch += 1
    # 反复调用前向传导并获得一系列结果
    rs, count = [self._get_activations(x[:single_batch]).pop()], single_batch
    while count < len(x):
        count += single_batch
        if count >= len(x):
            rs.append(self._get_activations(x[count - single_batch:]).pop())
        else:
            rs.append(self._get_activations(x[count - single_batch:count]).pop())
    # 利用np.vstack将这一系列结果进行合并
    return np.vstack(rs)

实现完毕后、我们就能得到如下图所示的结果（以在上一篇文章最后所用的螺旋线数据集上的训练过程为例）：

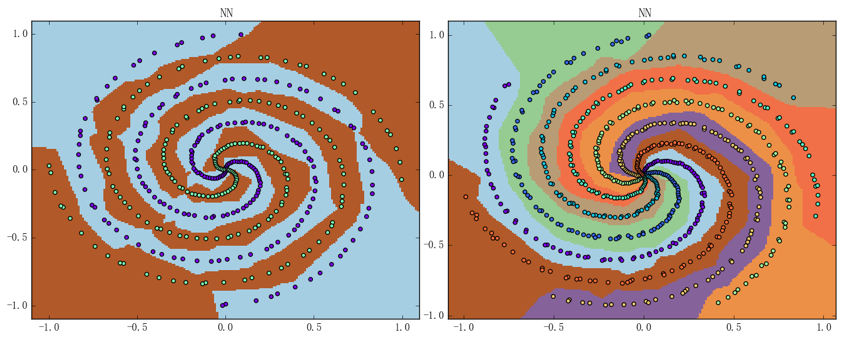
p1.png

其中左图的准确率为 99.0%、右图的准确率为 100%。神经网络的结构仍都是两层含 24 个神经元的 ReLU 加 SoftmaxCross Entropy 组合的这个结构、迭代次数仍为 1000 次、平均训练时间则分别变为 2.36秒（左图）和 3.84秒（右图）

交叉验证

由于针对现实任务训练出来的神经网络通常来说是很难直接进行可视化的，所以如果想要评估它的表现的话、就必须要用交叉验证。这里我们提供一种简易交叉验证的实现方法（以下代码需定义在fit方法中的相关位置、仅写出关键部分）：

1
2
3
4
5
6
7
8
9
10
11
# train_rate是传进来的参数、代表着训练集在整个数据集中占的比例
if train_rate is not None:
    train_rate = float(train_rate)
    train_len = int(len(x) * train_rate)
    shuffle_suffix = np.random.permutation(len(x))
    x, y = x[shuffle_suffix], y[shuffle_suffix]
    x_train, y_train = x[:train_len], y[:train_len]
    x_test, y_test = x[train_len:], y[train_len:]
else:
    x_train = x_test = x
    y_train = y_test = y

仅仅简单地把数据集分开并没有意义，如果想要进行评估的话、就必须切实利用到那分出来的测试集。一种常见的做法是实时记录模型在测试集上的表现并在最后以图表的形式画出，这正是我们之前展示过的各种训练曲线的由来；要想实现这种实时记录的功能、我们需要额外地定义一些属性和方法。思路大致如下：

  • 定义一个属性self._logs以存储我们的记录。该属性是一个字典、结构大致为： 其中和为训练集和测试集的实时表现
  • 常见的对模型实时表现的评估有三种：损失（cost）、准确率（acc）和 F1-score，其中前两种是通用的评估、F1-score 则针对二类分类问题（F1-score 的相关数学定义可以参见这里）
  • 定义三个方法，一个拿来实时记录这些评估、一个拿来输出最新的评估、一个拿来可视化评估

实现的话不难但繁、需要综合考虑许多东西并微调已有的代码；由于如果把所有变动的地方都写出来会有大量的冗余、所以这里就不写出所有细节了。感兴趣的观众老爷们可以尝试自己进行实现，我个人实现的版本则可以参见这里

实现完毕后、我们就能得到如下图所示的结果（以之前二分类螺旋线数据集上的训练过程为例）：

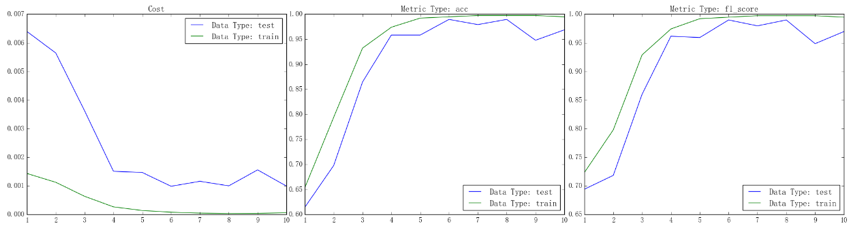
p2.png

从左到右依次为损失、准确率和 F1-score 的曲线，其中绿线为训练集上的表现、蓝线为测试集上的表现

进度条

当我们在解决现实生活中一个比较大型的问题时（比如网络爬虫或机器学习）、模型的耗时有时会达数十分钟甚至几个小时。在此期间如果程序什么都不输出的话、不免会感到些许不安：程序的运行到底到了哪个步骤？大概还需多久程序才能跑完呢？为了能在大型任务中获得即时的反馈、设计一个进度条是相当有必要的。本节拟介绍一种简单实用的进度条的实现方法，它支持记录并发程序的进度且损耗基本只来源于 Python 本身

先来看看我们的进度条是怎样的：

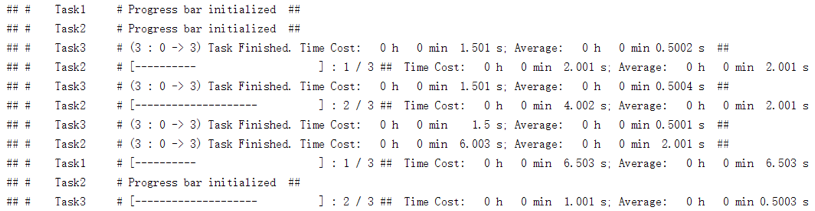
p3.png

其中每一行对应着一个单独任务的进度条、它有如下属性：

  • 任务名字（“Test”、“Test2”和“Test3”）
  • 一个形如“[- - - - - - ]”的进度显示器（紧跟在任务名字后面）
  • 已完成任务数和总任务数（紧跟在进度显示器后面、以 m /n 的形式出现，其中 m 为已完成任务数、n 为总任务数）
  • 总耗时和单个任务的平均耗时（紧跟在任务数后面，其中“Time Cost”后显示的是总耗时、“Average”后显示的是平均耗时，格式都是“时-分-秒”）

可以看到功能还算完备。不过虽说看上去有些复杂、但其实核心的实现只用到了time这个 Python 标准库和print这个 Python 自带的函数。总代码量虽说不算太大（110 行左右）、但有许多地方都是些琐碎的细节；所以我们这里就只说一个思路、具体的代码则可以参见这里

实现的大纲大概如下：

  • 要记录任务开始时的已完成的任务数和未完成的任务数
  • 要定义一个计数器，记录着总共已完成的任务数
  • 要定义一个start函数和一个update函数作为初始化进度条和更新进度条的接口
  • 要定义一个_flush函数来控制输出流

调用的方法也非常直观，这里举一个简单的例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
# 定义一个返回函数的函数
# 参数cost为任务耗时（秒）、epoch为迭代次数、name为任务名、_sub_task为子任务
def task(cost=0.5, epoch=3, name="", _sub_task=None):
    def _sub():
        bar = ProgressBar(max_value=epoch, name=name)
        # 调用start方法进行进度条的初始化
        bar.start()
        for _ in range(epoch):
            # 利用time.sleep方法模拟任务耗时
            time.sleep(cost)
            # 如果有子任务的话就执行子任务
            if _sub_task is not None:
                _sub_task()
            # 调用update方法更新进度条
            bar.update()
    return _sub
# 定义三个任务Task1、Task2、Task3
# 其中Task2、Task3分别为Task1、Task2的子任务
task(name="Task1", _sub_task=task(
    name="Task2", _sub_task=task(
        name="Task3")))()

这段代码的运行效果正如上图所示

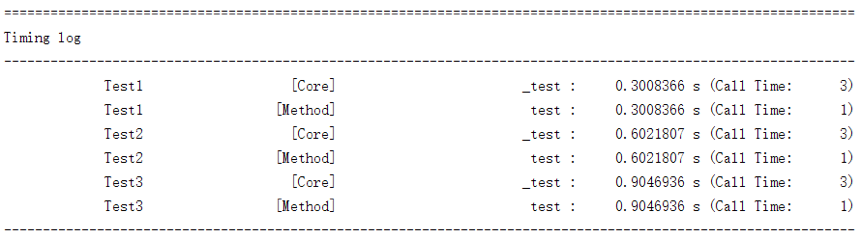
计时器

对于现实生活中的任务来说，我们往往需要让模型更可控、高效；这就使得我们需要知道程序运行的各个细节、或说各个部分的时间开销。Python 有一个自带的分析程序运行开销的工具 profile、它能满足我们大部分的要求。本节拟介绍 profile 的一种更灵活的轻量级替代品——Timing 的使用，其代码量仅 60 行左右、且可以比较简单地进行各种改进、拓展（Timing 的实现会放在今后介绍 Python 装饰器时进行简要的说明，观众老爷们也可以直接参见这里）

先来看一下它的效果：

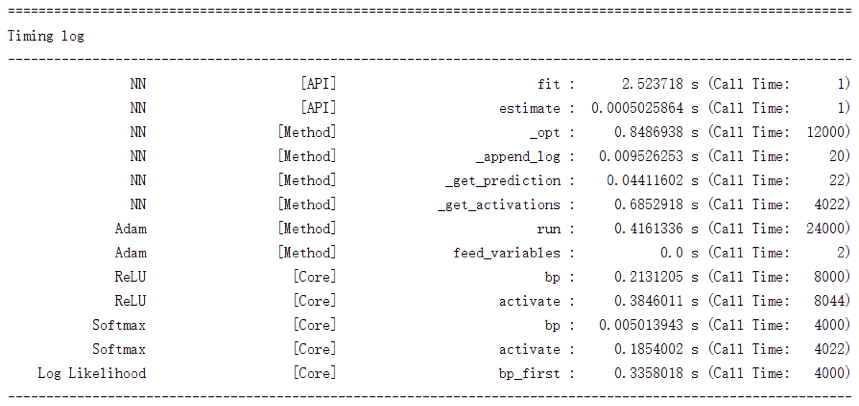
p4.png

该图反映的正是之前二分类螺旋线数据集上的训练过程。可以看到它将神经网络中各个组成部分的各个函数的开销情况都记录了下来、总体上来说已足够我们进行性能分析。此外、这里我们采取的是按名字排序，如有必要、完全可以定义成按总开销排序或是按平均开销排序（另外虽然我们没有记录平均开销、但是添加上平均开销这一项是平凡的）

应用 Timing 是比较简单的一件事，举一个小例子：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
# 定义一个测试类来进行简单的测试
class Test:
    timing = Timing()
    def __init__(self, rate):
        self.rate = rate
    # 以装饰器的形式、调用Timing中的timeit方法来计时
    # 默认迭代三次且单次迭代中调用self._test方法
    @timing.timeit()
    def test(self, cost=0.1, epoch=3):
        for _ in range(epoch):
            self._test(cost * self.rate)
    # 使用time.sleep模拟任务耗时
    @timing.timeit(prefix="[Core] ")
    def _test(self, cost):
        time.sleep(cost)
class Test1(Test):
    def __init__(self):
        Test.__init__(self, 1)
class Test2(Test):
    def __init__(self):
        Test.__init__(self, 2)
class Test3(Test):
    def __init__(self):
        Test.__init__(self, 3)
test1 = Test1()
test2 = Test2()
test3 = Test3()
test1.test()
test2.test()
test3.test()
test1.timing.show_timing_log()

这段代码的运行效果如下图所示：

p5.png
观众老爷们能赏个脸么 ( σ'ω')σ