评估与可视化

发表于 | 分类于

之前我们实现了一个 Node 基类CvDNode和一个 Tree 基类CvDBase；为了评估决策树模型的表现、我们需要先在这两个基类的基础上根据不同的算法实现出各种具体的决策树。由于我们在基类里面已经完成了绝大部分工作、所以在其上进行扩展是平凡的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class ID3Node(CvDNode):
    def __init__(self, *args, **kwargs):
        CvDNode.__init__(self, *args, **kwargs)
        self.criterion = "ent"
class C45Node(CvDNode):
    def __init__(self, *args, **kwargs):
        CvDNode.__init__(self, *args, **kwargs)
        self.criterion = "ratio"
class CartNode(CvDNode):
    def __init__(self, *args, **kwargs):
        CvDNode.__init__(self, *args, **kwargs)
        self.criterion = "gini"
        self.is_cart = True

在CvDBase的基础上定义三种算法对应的 Tree 结构的方法是类似的：

1
2
3
4
5
6
7
8
9
10
class ID3Tree(CvDBase, ID3Node, metaclass=CvDMeta):
    pass
class C45Tree(CvDBase, C45Node, metaclass=CvDMeta):
    pass
class CartTree(CvDBase, CartNode, metaclass=CvDMeta):
    pass

其中

1
2
3
4
5
6
7
8
9
10
11
12
class CvDMeta(type):
    def __new__(mcs, *args, **kwargs):
        name, bases, attr = args[:3]
        _, _node = bases
        def __init__(self, whether_continuous=None, max_depth=None, node=None, **_kwargs):
            tmp_node = node if isinstance(node, CvDNode) else _node
            CvDBase.__init__(self, whether_continuous, max_depth, tmp_node(**_kwargs))
            self._name = name
        attr["__init__"] = __init__
        return type(name, bases, attr)

接下来就是具体的评估与相应的可视化

我们同样可以使用蘑菇数据集来评估决策树模型的表现，结果如下所示：

蘑菇数据集上 ID3 算法的表现 蘑菇数据集上 C4.5 算法的表现 蘑菇数据集上 CART 算法的表现

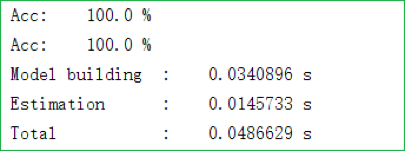
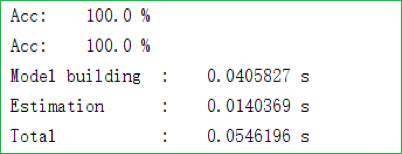
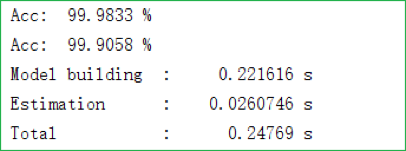
可以看到 CART 算法的表现相对来说要差不少，可能的原因有如下三条：

  • CART 算法在选择划分标准时是从所有二分标准里面进行选择的，这里就会比 ID3 和 C4.5 算法多出不少倍的运算量
  • 由于我们在实现 CART 剪枝算法时为了追求简洁、直接调用了标准库 copy 中的 deepcopy 方法对整颗决策树进行了深拷贝。这一步可能会连不必要的东西也进行了拷贝、从而导致了一些不必要的开销
  • CART 算法生成的是二叉决策树，所以可能生成出来的树会更深、各叶节点中的样本数可能也会分布得比较均匀、从而无论是建模过程还是预测过程都会要慢一些

当然，如果结合蘑菇数据集来说的话、笔者认为最大的问题在于：CART 算法不适合应用于蘑菇数据集。一方面是因为蘑菇数据集全是离散型特征且各特征取值都挺多，另一方面是因为蘑菇数据集相对简单、有一些特征非常具有代表性（我们在说明朴素贝叶斯时也有所提及），仅仅用二分标准划分数据的话、会显得比较没有效率

为了更客观地评估我们模型的表现，我们可以对成熟第三方库 sklearn 中的决策树模型进行恰当的封装并看看它在蘑菇数据集上的表现：

蘑菇数据集上 sklearn 决策树的表现（criterion=entropy） 蘑菇数据集上 sklearn 决策树的表现（criterion=gini）

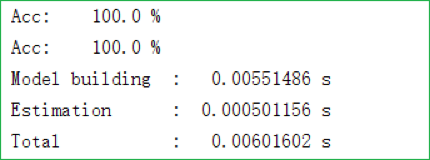
不得不承认、成熟第三方库的效率确实要高很多（比我们的要快 5 倍左右）；这是因为虽然算法思想可能大致相同，但 sklearn 的核心实现都经过了高度优化、且（如不出意料的话）应该都是用 C 或者其它底层语言直接写的。不过正如第一章说过的，要想应用 sklearn 中的决策树、就必须先将数据数值化（即使是离散型数据）；而我们实现的决策树在处理离散型数据时却无需这一步数据预处理、可以直接应用在原始数据上（但处理混合型数据时还是要先进行数值化处理、而且将离散型数据数值化也能显著提升模型的运行速度）

我们在本系列的综述里面曾说过、决策树可能是从直观上最好理解的模型；事实上，我们之前画过的一些决策树示意图也确实非常直观易懂、于是我们可能自然就会希望程序能将生成类似的东西。虽然不能做到那么漂亮、不过我们确实是能在之前实现的决策树模型的基础上做出类似效果的：

蘑菇数据集上 ID3 决策树的可视化 蘑菇数据集上 C4.5 决策树的可视化 蘑菇数据集上 CART 决策树的可视化

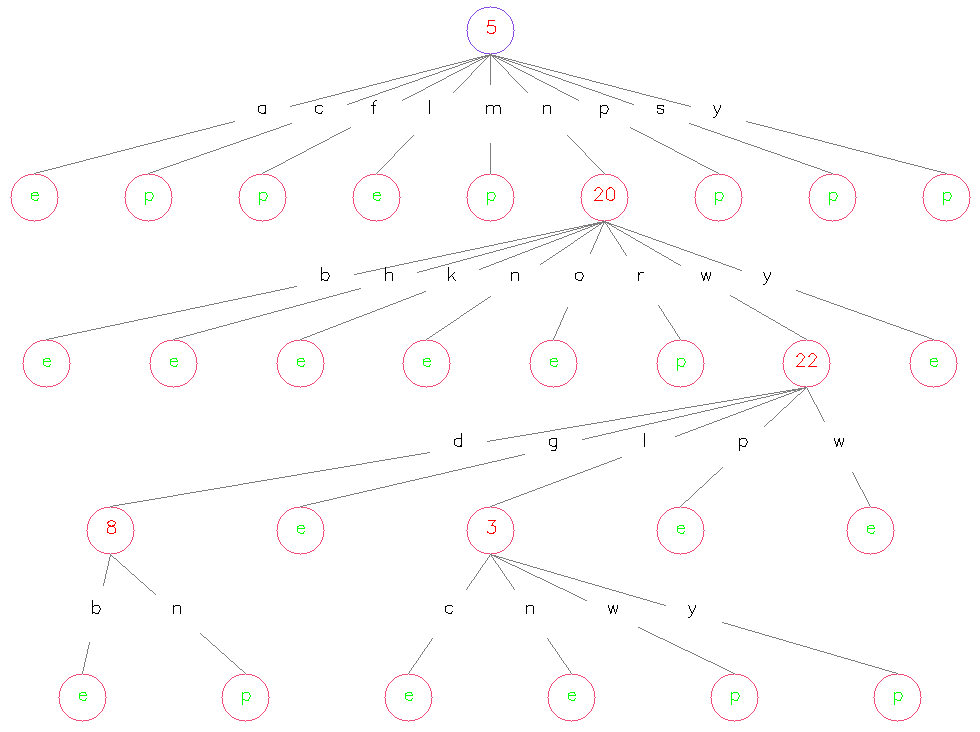
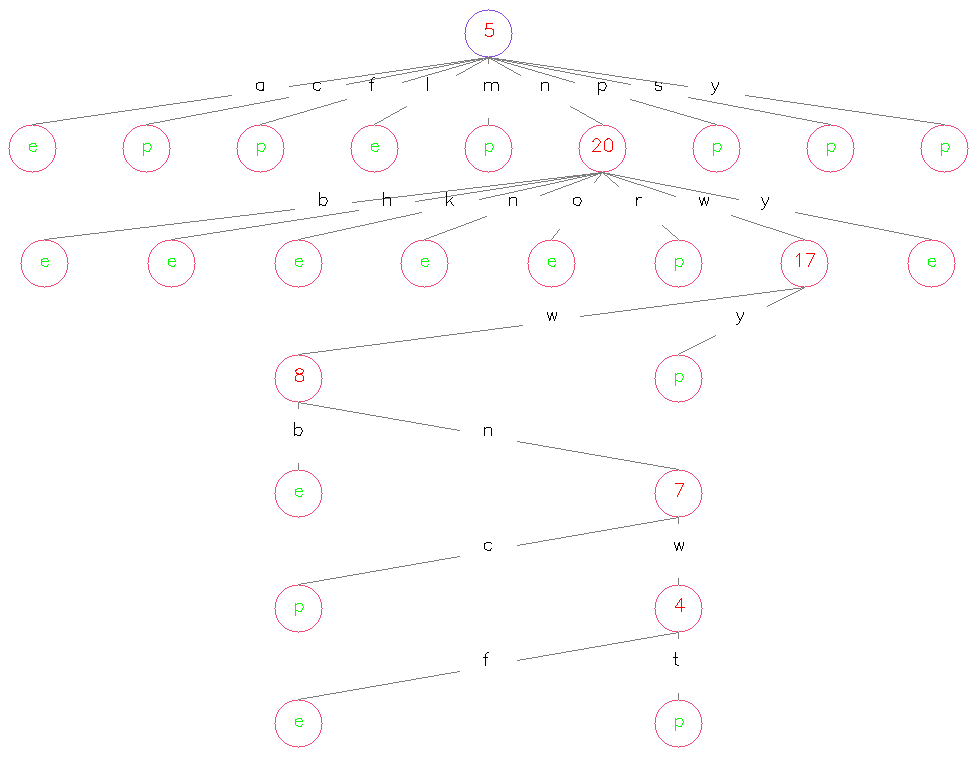
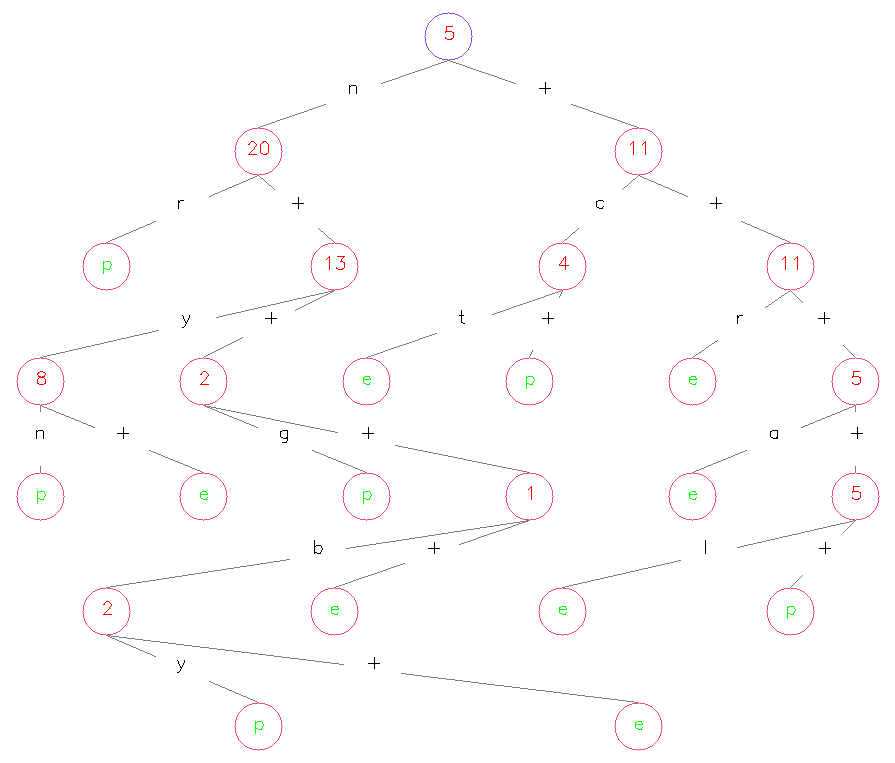
其中，红色数字代表该 Node 作为划分标准的特征所属的维度，位于各条连线中央的字母代表着该维度特征的各个取值、加号“+”代表着“其它”，绿色字母代表类别标记。以上三张图在一定程度上验证了我们之前的很多说法，比如说 ID3 会倾向选择取值比较多的特征、C4.5 可能会倾向选择取值比较少的特征且倾向于在每个二叉分枝处留下一个小 Node 作为叶节点、CART 各个叶节点上的样本分布较均匀且生成出的决策树会比较深……等等

我们在说明朴素贝叶斯时曾经提过，即使只根据第 5 维的取值来进行类别的判定、最后的准确率也一定会非常高。验证这一命题的方法很简单——只需将决策树的最大深度设为 1 即可，结果如下图所示：

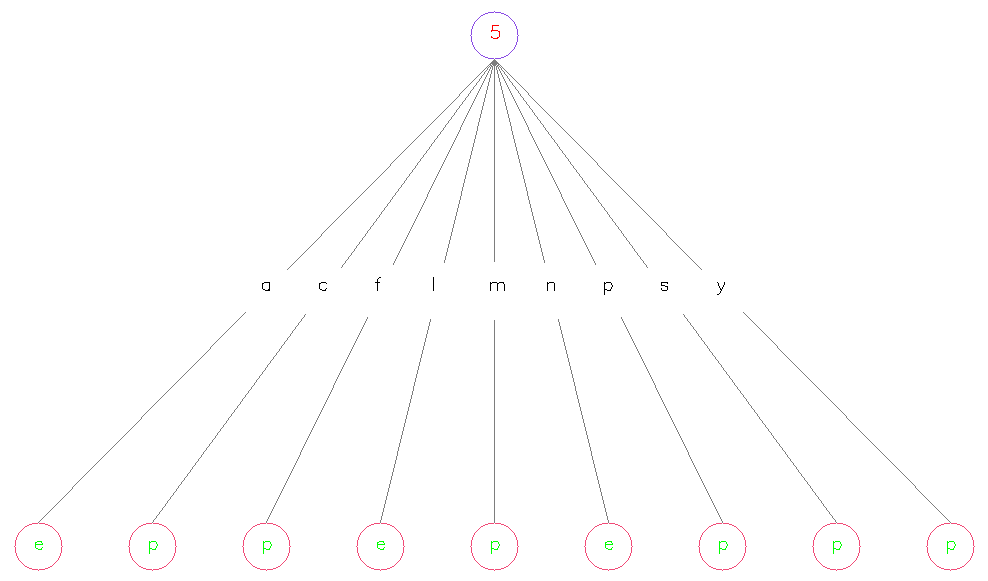
p9.png

此时模型的表现如下图所示：

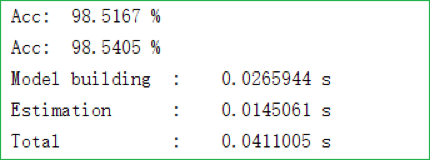
p10.png

可以看到其表现确实不错。值得一提的是，单层决策树又可称为“决策树桩（Decision Stump）”、它是有特殊应用场景的（比如我们在下个系列中讲 AdaBoost 时就会用到它）

至今为止我们用到的数据集都是离散型数据集，为了更全面地进行评估、使用连续型混合型数据集进行评估是有必要的；同时为了增强直观、我们可以用异或数据集来进行评估。原始数据集如下图所示：

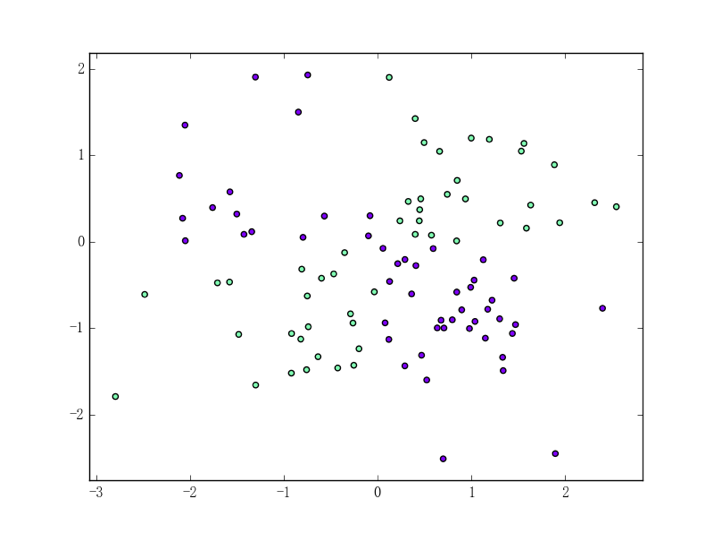
p11.png

生成异或数据集（及其它二维数据集）的代码定义在之前提过 DataUtil 类中（可参见这里），读者也可以在下一章中找到相应的讲解。为使评估更具有直观性、我们可以把四种决策树（ID3、C4.5、CART 决策树和 sklearn 的决策树）在异或数据集上的表现直接画出来：

异或数据集上 ID3、CART 和 sklearn 决策树的表现 异或数据集上 C4.5 决策树的表现

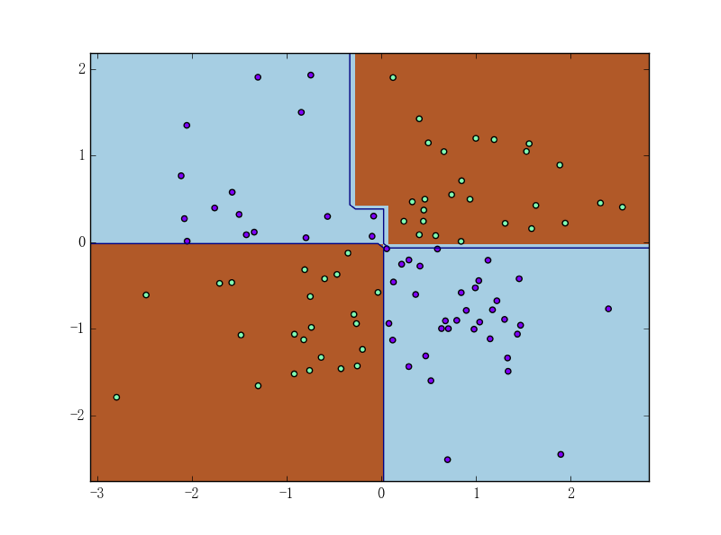
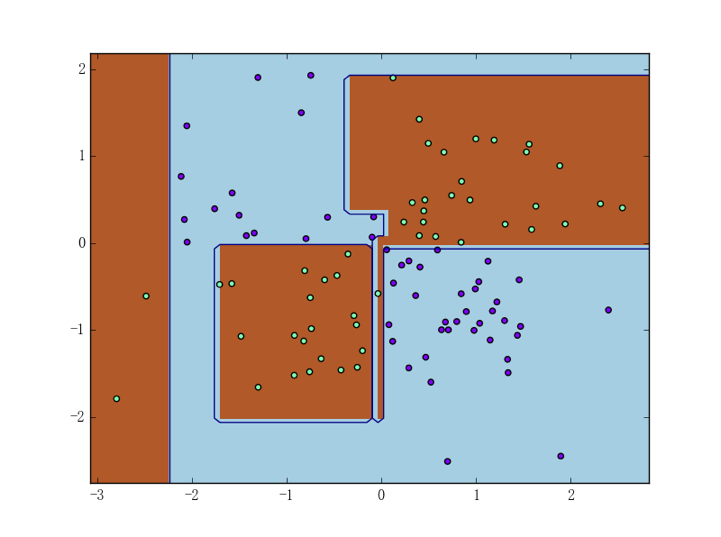
可以看到 C4.5 决策树的过拟合现象比较严重。正如我们之前所分析的一般、这很有可能是因为 C4.5 在二叉分枝时会倾向于进行“不均匀的二分”（从上图也可以大概看出）

观众老爷们能赏个脸么 ( σ'ω')σ